The U.S. Common Core State Standards in Mathematics mentions the use of tape diagrams to visualize relationships between quantities and to solve mathematical problems. Such a diagram is simply a “one-dimensional” version of the area model, using a strip of paper to represent quantities. Tape diagrams are also known as strip diagrams and bar diagrams and are used in a number of curriculums about the globe. Search on the internet for “tape diagrams” and a plethora of materials will be revealed to you.

As a first example, this picture compares the quantities \(32\) and \(17\).

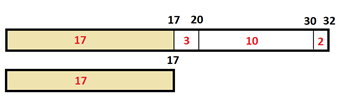
It shows that the two numbers differ by \(3+10+2=15\).  Thus we see \(32-17=15\).

Alternatively, we can reason via the diagram that \(32-17\) is the same as \(30-15=15\).

Or better yet, that \(32-17\) is the same as \(\left(32-3\right)-\left(17-3\right)\), which allows us to avoid carries if we like the traditional subtraction algorithm and want to use it.

Comment: Seeing that \(1005-276\) is equivalent to \(999-270\) is lovely with regard to using the traditional algorithm.

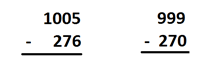
Tape diagrams are a wonderful tool in the K-5 curriculum for developing true number sense, especially with fractions and percentages.

 

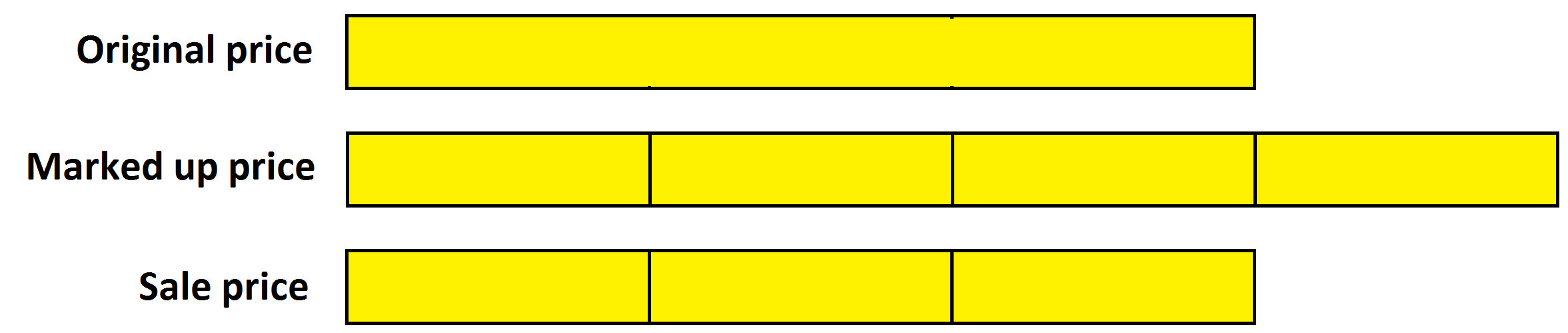
EXAMPLE: I am a dishonest person. I’ll buy a computer with the intent of reselling it, but I’ll mark up its price by a third and then say it’s on sale,  \(25\%\) off its marked price. (Hee hee hee.) How much profit do I expect to make? 

Answer: I see I make no profit. (Serves me right!)

 

Do look at the internet for many examples of this work.

 

RATIO PROBLEMS

Tape diagrams often help with schoolbook ratio problems.

(Recall that these notes are written for educators. The sample of problems below give a swift overview of the type of material that can be addressed with tape diagrams. Setting up proper student understanding of “ratio” and “percentage increase,” and so on, needs to conducted carefully and slowly.)

 

EXAMPLE: There are \(35\) students in a class. The ratio of boys to girls in the class is \(2:5\). How many more girls are there than boys?

Answer: For every two groups of boys there are a matching five groups of girls.

 

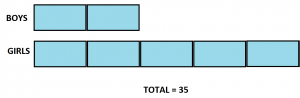
The diagram shows that we can think of the class as divided into a total of seven groups. There are thus \(5\) students per each of these groups. As there are three more groups of girls than boys, there are a total of \(3 \times 5 =15\) more girls than boys.

 

EXAMPLE: Ms. Dubolt has twice as much money as Ms. Fortitude. Ms. Fortitude has only \(80\%\) as much money as Ms. Grizwald. What is the ratio of Ms. Dubolt’s worth to Ms. Grizwald’s?

Answer:

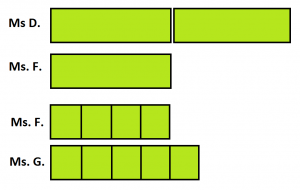
We see that Ms. D.s wealth is eight parts to Ms. G.s five parts. The ratio of their cash wealth is \(8:5\).

 

EXAMPLE: Box A contains \(33\frac{1}{3}\%\) more apples than box B. If half the apples are taken from

Box A and moved to box B, what will be the ratio of the number of apples in box A to the number in box B?

Answer:

 

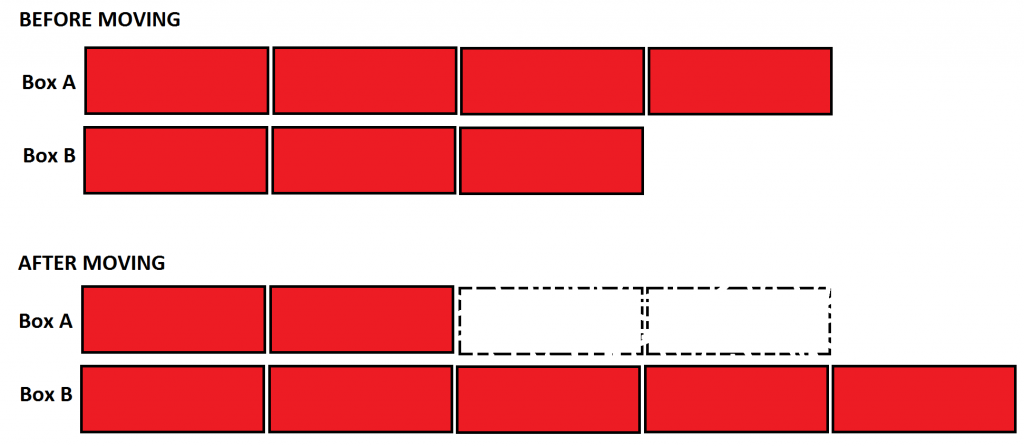
The new ratio is \(2:5\).

 

EXAMPLE: Albert and Bilbert collected seashells. Albert collected only half as many seashells as Bilbert. When Bilbert asked how many seashells Albert had, he lied and gave a number that was three more than he really had. Bilbert responded: “Oh, so the number of shells you collected compared to the number I collected are in a 3:4 ratio.”  How many shells did Albert actually collect?

Answer:

In the picture that is a lie, Albert supposedly has three groups of a quantity and Bilbert four. Divide each of Bilbert’s blocks in half and he has four half blocks. Thus Albert has three half blocks, with the three shells, supposedly, making half a block. Thus each block contains six shells.

Looking at the truthful picture we see that Albert collected in reality six shells.

 

EXAMPLE: Cuthbert and Dilbert were given equal amounts of cash. After Cuthbert spent $55 and Dibert spent $25, the ratio of Cuthbert’s cash to Dilbert’s was \(4:7\). How much money was each lad given initially?

Answer:

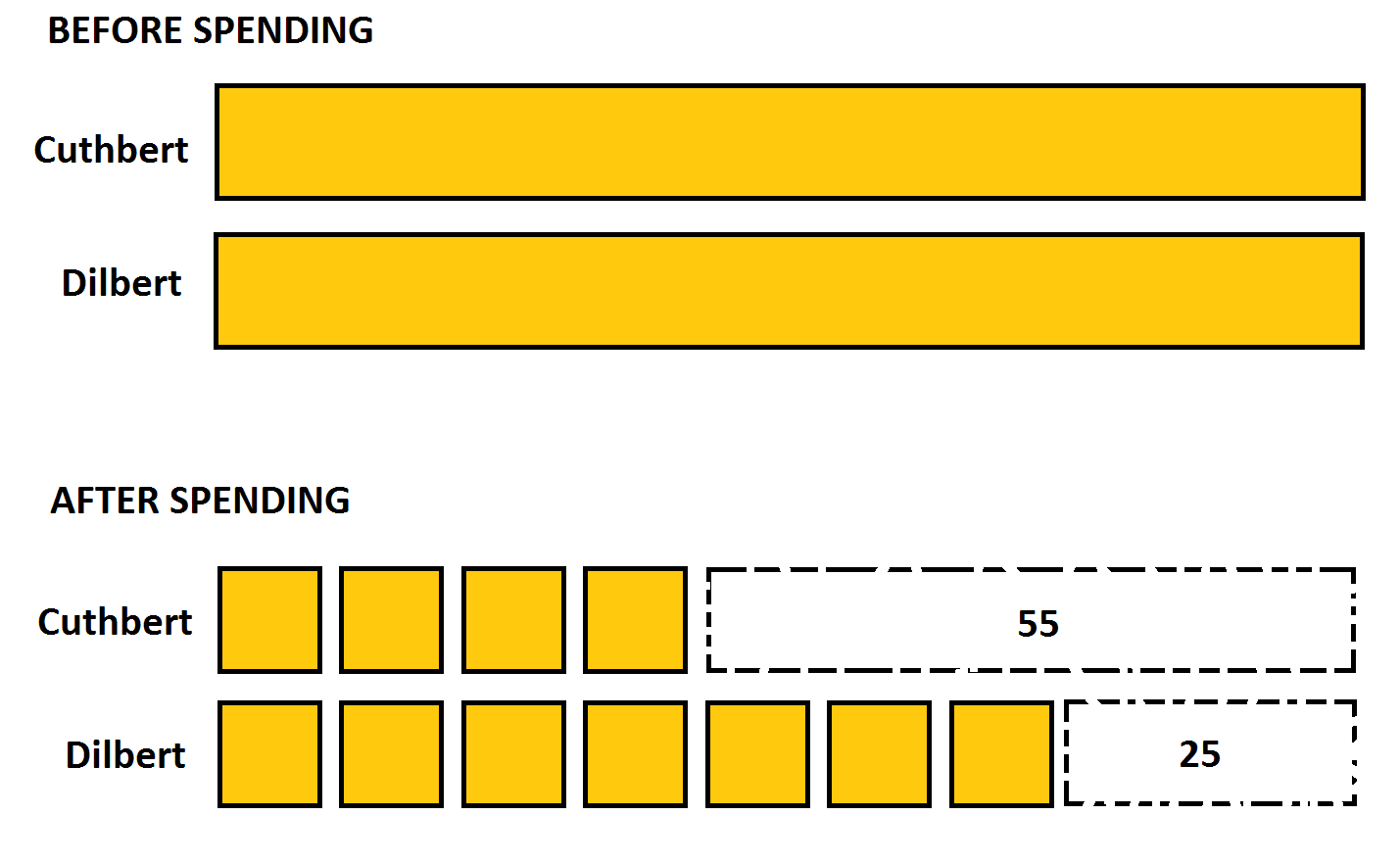
In the second diagram we see that three blocks match the difference of $30. So each block is worth $10 and Cuthbert was initially given \($40+$55=$95\), as was Dilbert (\($70+$25\)).

 

 

EXAMPLE: Egbert and Filbert each have cash in their wallets. Their cash amounts are in a \(6:11\) ratio with Filbert possessing more cash than Egbert. The men go on a shopping spree. Egbert spends half his money and Filbert spends $20, leaving Filbert now with triple the amount of cash than Egbert. How much money did Egbert spend on the shopping spree?

Answer:

 

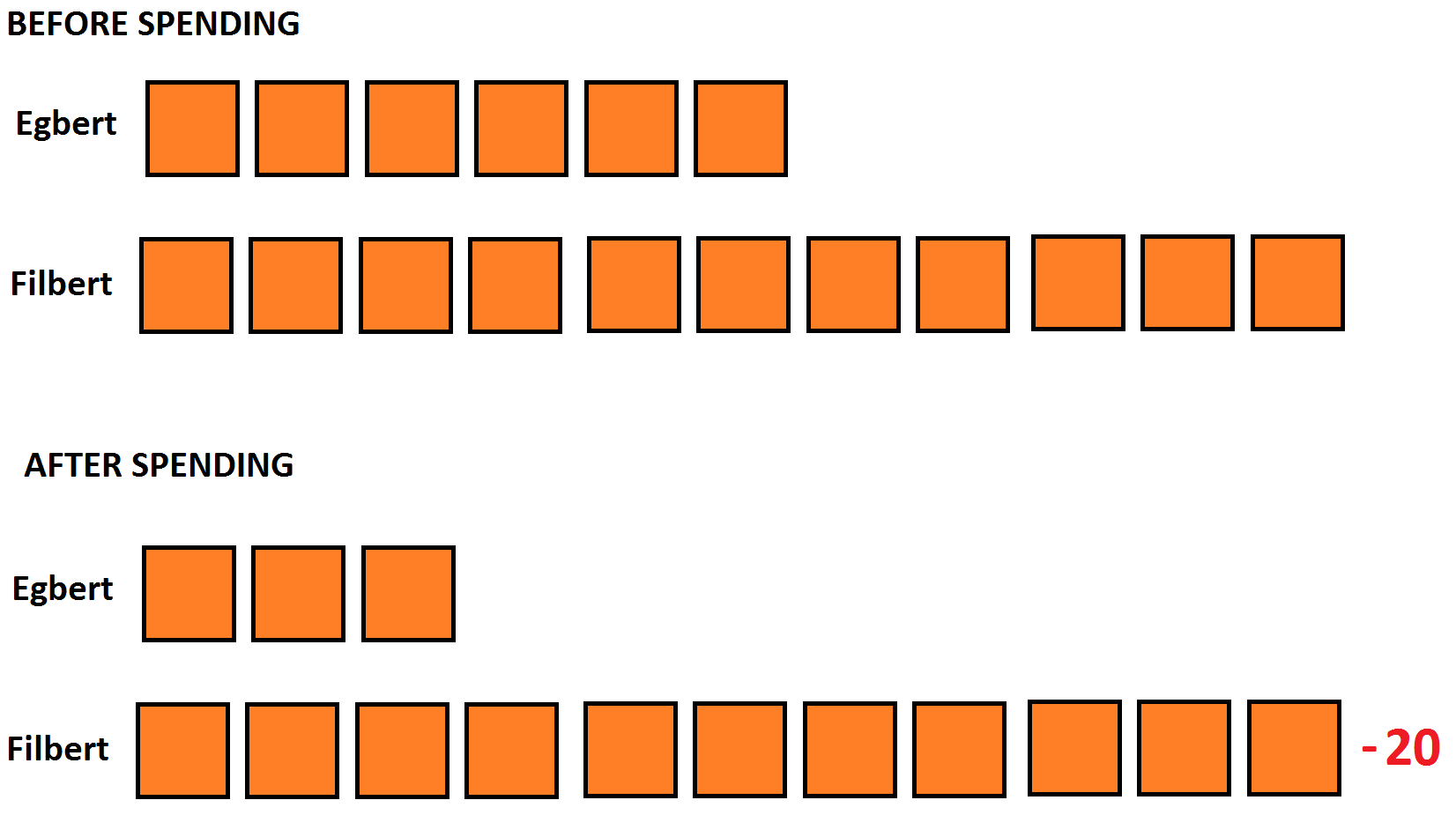
Before spending, Egbert has six blocks of cash and Filbert eleven. After spending, Ebgert has three and Filbert triple this, which must be nine. Thus the $20 Filbert spent matches two blocks of cash. Each block is thus worth $10 and Egbert, having spent three blocks worth, spent a total of $30.

 

EXAMPLE: I have a supply of lemon candies and lime candies, with the ratio of lemon to lime candies being \(3:2\). I eat \(10\) lemon candies and the ratio of lemon to lime candies is now \(2:3\). How many candies did I have in total to begin with?

Answer:

It is hard to make sense of “after” diagram.

The  \(2:3\) ratio says we must think of the count of lemon candies that remain as two blocks and the count of lime candies as three blocks. Let’s divide each of the green blocks into thirds.

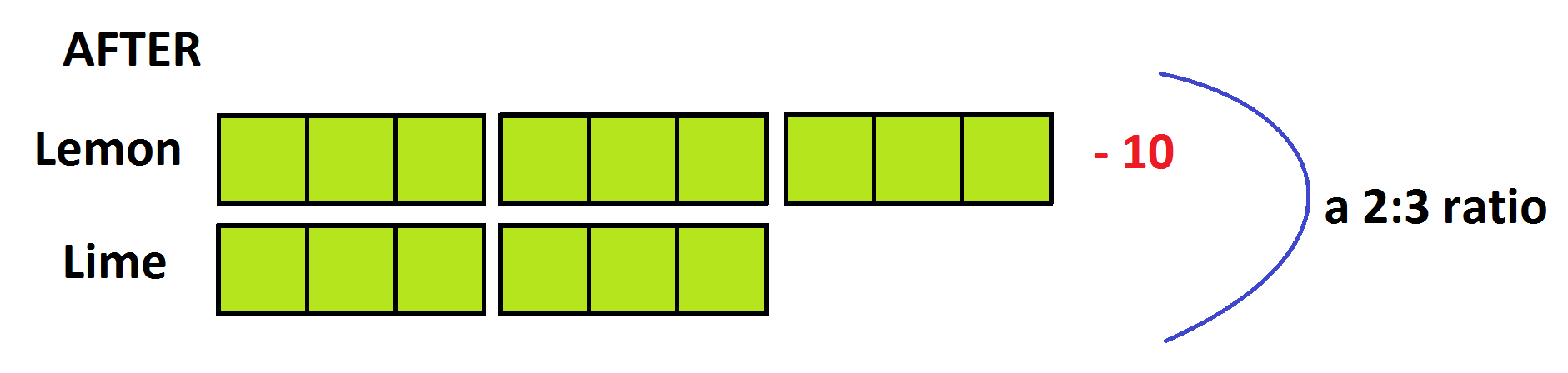
So the count of limes is \(6\) third-blocks. Thus the count of lemon candies must be \(4\) third-blocks. This means that the ten candies removed must match five third-blocks.

So each third-block is worth two candies, and each original full green block six candies.

Thus we initially had \(3\times 6=18\) lemon candies and \(2 \times 6 =12\) lime candies for a total of \(30\) candies.

 

SYSTEMS OF EQUATIONS

EXAMPLE: Three bananas and two pears cost $3.45 . Two bananas and one pear cost $2.10. What is the cost of a banana?

Answer:

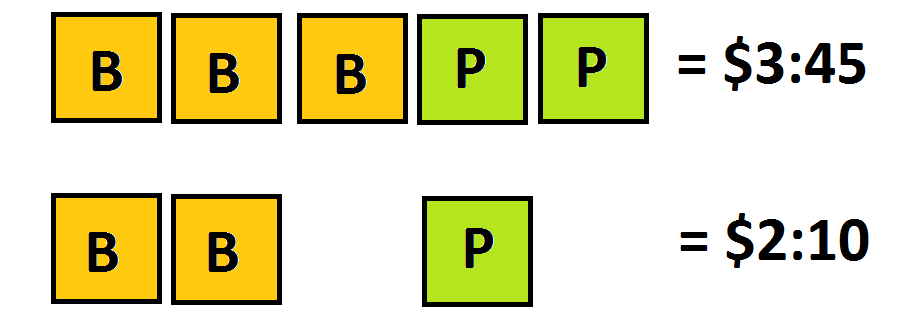
We see from the diagrams that a banana and a pair together must cost \(3.45-2.10=$1.35\).

From the bottom diagram this means that a single banana must cost \(2.10-1.35=$0.75\).

 

This next one is intellectually juicy. Try it before scrolling down to the solution.

EXAMPLE:  There are \(37\) people in a room. One third of the men and \(40\%\) of the woman are Australian, making for a total of \(14\) Australians in the room. How many Australian men are there and how many Australian women are there?

 

 

 

 

 

 

 

 

 

 

 

 

 

EXAMPLE:  There are \(37\) people in a room. One third of the men and \(40\%\) of the woman are Australian, making for a total of \(14\) Australians in the room. How many Australian men are there and how many Australian women are there?

Answer: We don’t know the block sizes for the men and for the women in the schematic below. But we have three equal-sized blocks for the men, with one all Australian, and five equal-sized blocks for the women, with two all Australian.

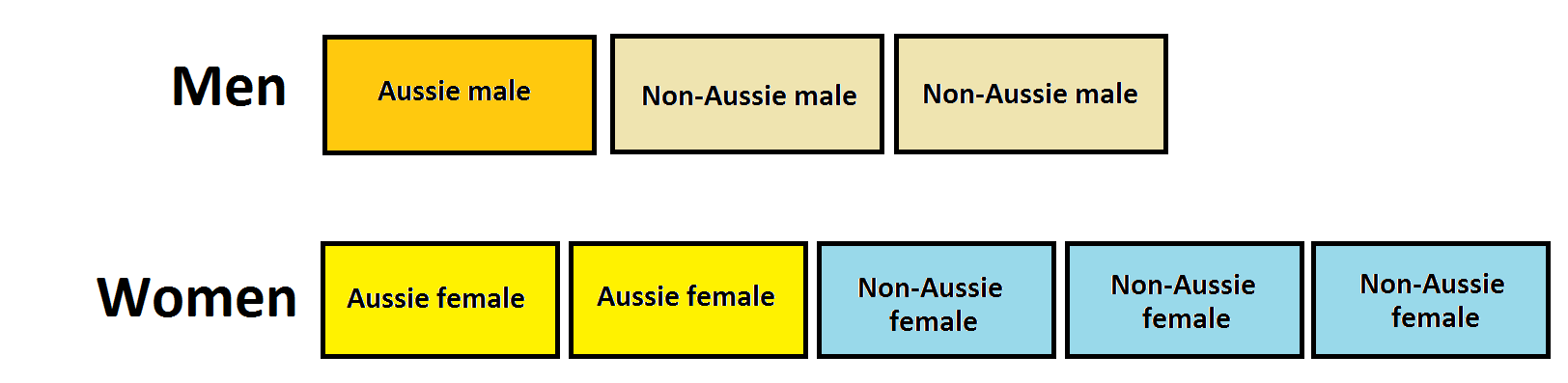
We are told that all the eight blocks represent \(37\) people and that

But all the male blocks are the same size, as are all the female blocks.

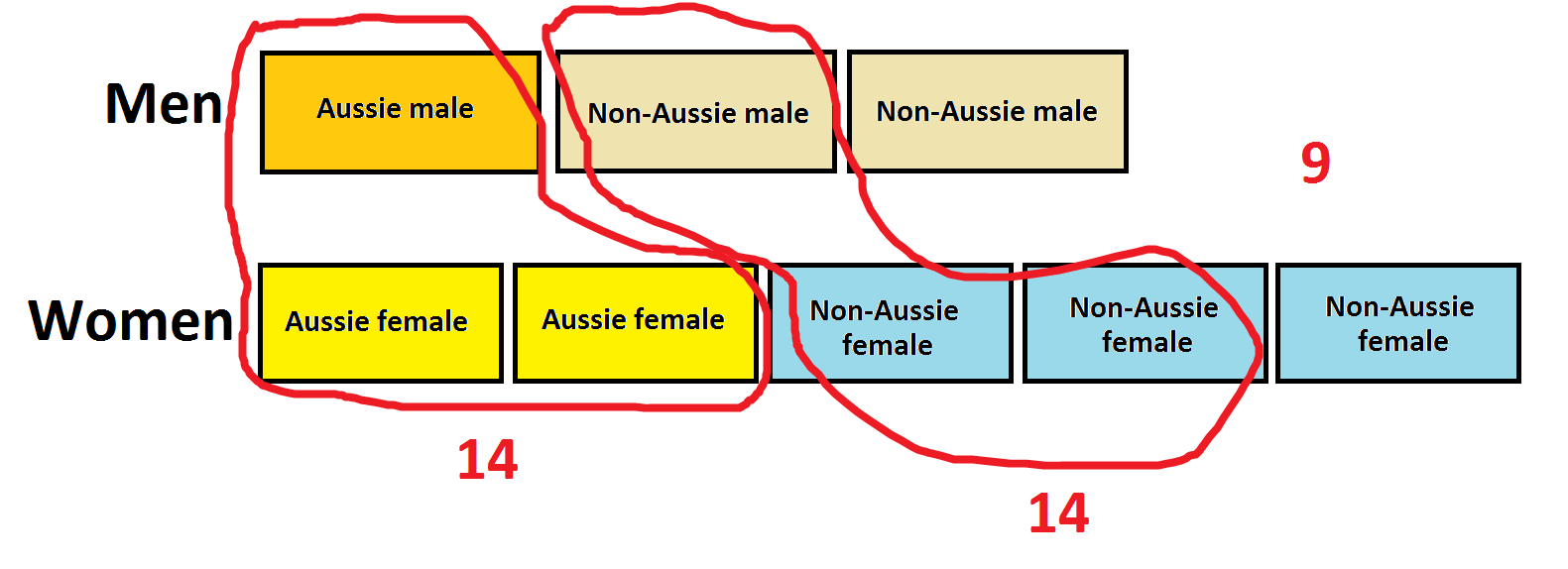
We thus see that one block for the men and one block for the women together account for \(9\) people. Looking at the set of Australians we now see that one block for the women accounts for \(5\) women. Consequently each block for the men accounts for \(9-5=4\) men.

There are \(4\) Australian men and \(2 \times 5=10\) Australian women in the room.

 

Pedagogical Comment: Have students create problems like these too. Constructing exercises is hard and it deepens the learning experience profoundly.

Resources