It is not always part of the curriculum to have students divide polynomials that leave remainders. This section is thus optional.

 

In my work with students I develop two approaches for dividing polynomials: dividing via exploding dots  and dividing via the reverse area method.

The exploding dots method is conceptually straightforward (almost alarming so) and even if remainders are involved it is absolutely visually clear what to do with them. The disadvantage of the Exploding Dots approach, however, is that it is not paper-and-pencil friendly. (Drawing those dots is tiresome!)

The reverse area method is quick and easy to conduct with paper-and-pencil, but has the disadvantage that it is not quite as clear how to handle remainders if they appear. It is not hard to think one’s way through them when they do occur, but one does have to do that extra step of thinking.

Let me explain.

 

The reverse area method shows that \(\dfrac{x^{2}+5x+6}{x+2}\) equals \(x+3\), that is, that \(x^{2}+5x+6\) is evenly divisible by \(x+2\). Consequently, \(x^{2}+5x+10\) is not evenly divisible by \(x+2\), it will leave a remainder of \(4\).  How does this remainder manifest itself when we try the reverse area method?

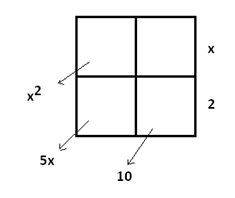
Since we expect to see a constant-term remainder, let’s start filling the table at the top-left corner and work from left to right, making sure the \(x^{2}\) and \(x\) terms are properly matched.

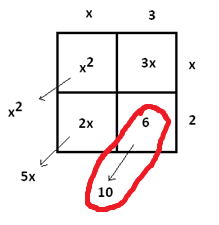
Doing this we see a mismatch (of four) with the constant terms. How do we interpret the mismatch?

 

The table “wants” the constant term to be \(6\) and if it were, the table computes \(\dfrac{x^{2}+5x+6}{x+2}=x+3\).  But we have \(\dfrac{x^{2}+5x+10}{x+2}\).

 

But we have to deal with what we’ve got. So let’s deal with it by making the ideal computation appear in what we have.

\(\dfrac{x^{2}+5x+10}{x+2}=\dfrac{x^2+5x+6+4}{x+2}=\dfrac{x^2+5x+6}{x+2}+\dfrac{4}{x+2}=x+3+\dfrac{4}{x+2}\).

(Multiply through by \(x+2\), if you like, to check this.)

 

 

Another example. Consider \(\dfrac{x^{4}+x^{3}+x^{2}+x+1}{x^{2}+x+2}\).

Starting at the top left cell to “push” all the remainders into lower order cells, we get:

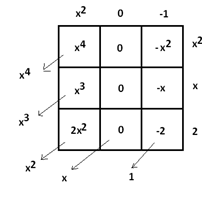
There is a mismatch in both the \(x\) and the constant terms. The table shows \(\dfrac{x^{4}+x^{3}+x^{2}-x-2}{x^{2}+x+2}=x^{2}-1\).

Looking at what we have and comparing it to what the table wants, we see:

 

\(\dfrac{x^{4}+x^{3}+x^{2}+x+1}{x^{2}+x+2}=\dfrac{x^{4}+x^{3}+x^{2}-x-2+2x+3}{x^{2}+x+2}\)

\(=x^{2}-1+\dfrac{2x+3}{x^{2}+x+2}\).

 

MUST WE START AT THE TOP LEFT CORNER?

Look again at  \(\dfrac{x^{2}+5x+10}{x+2}\)  but this time let’s compute it by starting at the bottom right corner of its table. 

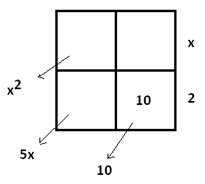
This time it gives \(\dfrac{x^{2}+5x+10}{x+2} = \dfrac{x^{2}}{x+2}+5\), which is valid and correct. In fact, some algebraic work shows that this is equivalent to our previous answer:

\(\dfrac{x^{2}}{x+2}+5 = \dfrac{x^{2}+2x-2x-4+4}{x+2}+5\)

\(= \dfrac{x\left(x+2\right)}{x+2}+\dfrac{-2x-4}{x+2}+\dfrac{4}{x+2}+5 = x-2 + 5 + \dfrac{4}{x+2}\)

\(= x+3+\dfrac{4}{x+2}\).

 

Starting at the top left corner makes sure that higher degrees terms match giving a final answer with a remainder expressed in lower degree terms. Starting at the bottom right corner makes sure that lower degree terms match giving a final answer with a remainder expressed in high degree terms. All results are algebraically equivalent. But it is generally preferred,that if you feel the need to conduct a polynomial division, to have a final result with any ratio terms expressed as a polynomial of low degree divided over a polynomial of higher degree. (It allows one to identify asymptotes when graphing rational functions by hand.) For this reason it is standard practice to compute all polynomial divisions by starting at the top left cell.

 

EXERCISE 1:

a) Compute \(\dfrac{x^{6}-x^{4}+x^{3}}{x^{2}-1}\)

 

b) Compute \(\dfrac{2x^{5}+x^{4}+3x^{3}-2x^{2}+x+1}{x^{2}+x+1}\)

 

EXERCISE 2:

a) Show that \(\dfrac{x^{2}-6x+11}{x-2}\) equals \(x-4+\dfrac{3}{x-2}\).

 

b) Compute \(\dfrac{x^{2}+x+1}{x-5}\)

 

c) Compute \(\dfrac{2x^{2}+15x-63}{x+10}\)

 

d) Explain the following:

A quadratic \(ax^{2}+bx+c\) divided by a linear term \(x-h\) is sure to be of the form \(\dfrac{ax^{2}+bx+c}{x-h}=Ax+B+\dfrac{d}{x-h}\) with \(A\), \(B\), and \(d\) real numbers.

 

In fact, go further and use the reverse area method to show that:

\(A=a\)

\(B=ah+b\)

\(d=ah^2+bh+c\)

(Notice that \(d=ah^{2}+bh+c\) is the value of the quadratic at \(x=h\).

 

e) Explain the following: If a quadratic \(ax^{2}+bx+c\) has value \(0\) at \(x=h\), then \(x-h\) is a factor of the quadratic.

 

Comment: This result is a special case of the Remainder Theorem coming up in the next lesson.

 

EXERCISE SOLUTIONS

1. a) \(x^{4}+x+\dfrac{x}{x^{2}-1}\)  b) \(2x^{3}-x^{2}+2x-3+\dfrac{2x+4}{x^{2}+x+1}\)

2. a) It does!   b) \(x+6+\dfrac{31}{x-5}\)   c) \(5x-35+\dfrac{287}{x+10}\)

d)

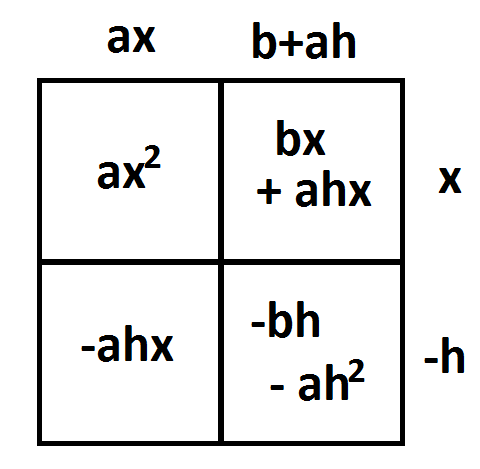
\(\dfrac{ax^{2}+bx+c}{x-h}=\dfrac{ax^{2}+bx+\left(-ah^{2}-bh\right)+ah^{2}+bh+c}{x-h}=ax+\left(ah+b\right)+\dfrac{ah^{2}+bh+c}{x-h}\).

 

e) If the quadratic is zero at \(x=h\), then \(ah^{2}+bh+c=0\), and so \(\dfrac{ax^{2}+bx+c}{x-h}=ax+(ah+b)+0\). That is, \(ax^{2}+bx+c =\left(x-h\right)\left(ax+ah+b\right)\) and \(x-h\) is a factor of \(ax^{2}+bx+c\).

(And conversely, if \(x-h\) is a factor of a quadratic, \(ax^{2}+bx+c=\left(x-h\right)\left(px+q\right)\), then that quadratic has value \(0\) at \(x=h\).)

Resources