4.6 The Infamous Boy-Boy Paradox

The Astounding Power of Area

4.6 The Infamous Boy-Boy Paradox

Course Home

Here is a famous puzzle that befuddled the best of mathematical minds (including Martin Gardner). It also snagged me when I first thought about it.

Consider three scenarios:

Albert, who you just met, tells you that he has two children and that his oldest child is a boy. What are chances that his other child is also a boy?

Bilbert, who you also just met, tells you that he has two children and that one of his children is a boy. What are the chances that his other child is also a boy?

Cuthbert, also a new acquaintance, tells you he has two children and that one of his children is a boy and was born on a Tuesday. What are the chances that his other child is also a boy?

The usual answers presented are, in turn, \(\dfrac{1}{2}\), \(\dfrac{1}{3}\), and \(\dfrac{13}{27}\), which are mighty strange, and hence paradoxical. Surely the answer is 50% in each and every case with the chance of a second child being male being fifty-fifty? (The extra information supplied in the final two scenarios is surely just extraneous?)

The trouble is, one can legitimately argue that the answers given are incorrect! This then supplies a paradox within the paradox, the feature that snags the professionals too. Let me explain.

Assume that giving birth to a child of any particular gender is equally likely.

Let’s imagine we encountered \(196\) men with first and second children. (I chose the number \(196\) after some trial and error. It is a number that allows me to avoid fractional counts of children in the table I am about to create.)

Among the \(196\) men, we’d expect half, \(98\) of them, to have oldest child a boy. Of those \(98\), we’d expect half, \(49\) of them, to have youngest child a boy. In fact, in general, we’d expect \(49\) men with each possible gender pair: boy-boy, boy-girl, girl-boy, girl-girl.

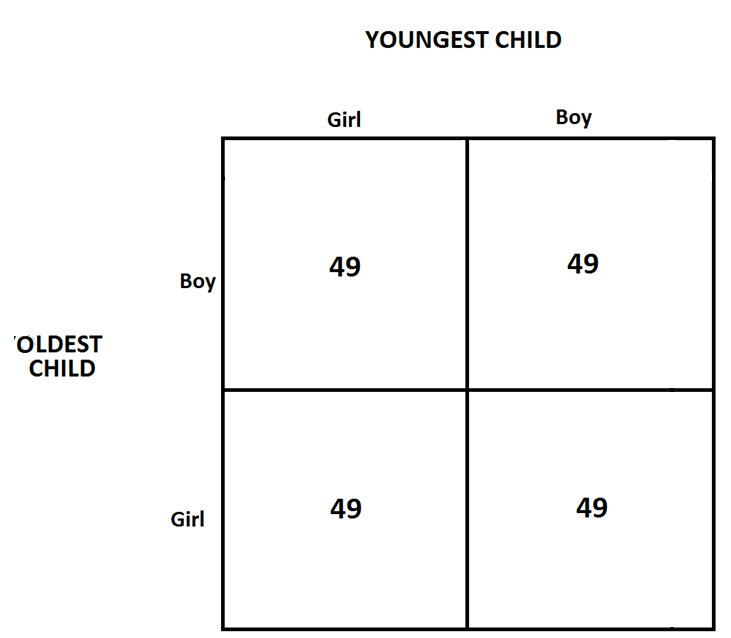
Albert tells you he is among the 98 men with oldest child a boy. The chances that he is among the subset of 49 men with youngest child also a boy is 50%.

So far, so good.

But a rub comes with Bilbert’s statement as we are not told which child he commented on. Let’s assume that Bilbert chose a child at random, each equally likely to be chosen (he secretly flipped a coin, say) and then mentioned the gender of that child. We now reason:

There are \(49+49=98\) men with a child of each gender and we expect half of them, that is, 49 of them, to say “one of my children is a boy” after the flip of a coin. The 49 men with two boys will for sure say “one of my children is a boy.” Bilbert tells us that he is among the 98 men who say these words. The chances that he is among the subset of 49 men with two boys is 50%.

Now on to Cuthbert:

We’d expect in any group of boys \(\dfrac{1}{7}\) of them to be born on a Tuesday and in any collection of boy-boy pairs, \(\dfrac{1}{49}\) of them to both be born on a Tuesday. Here is the refined table to reflect this.

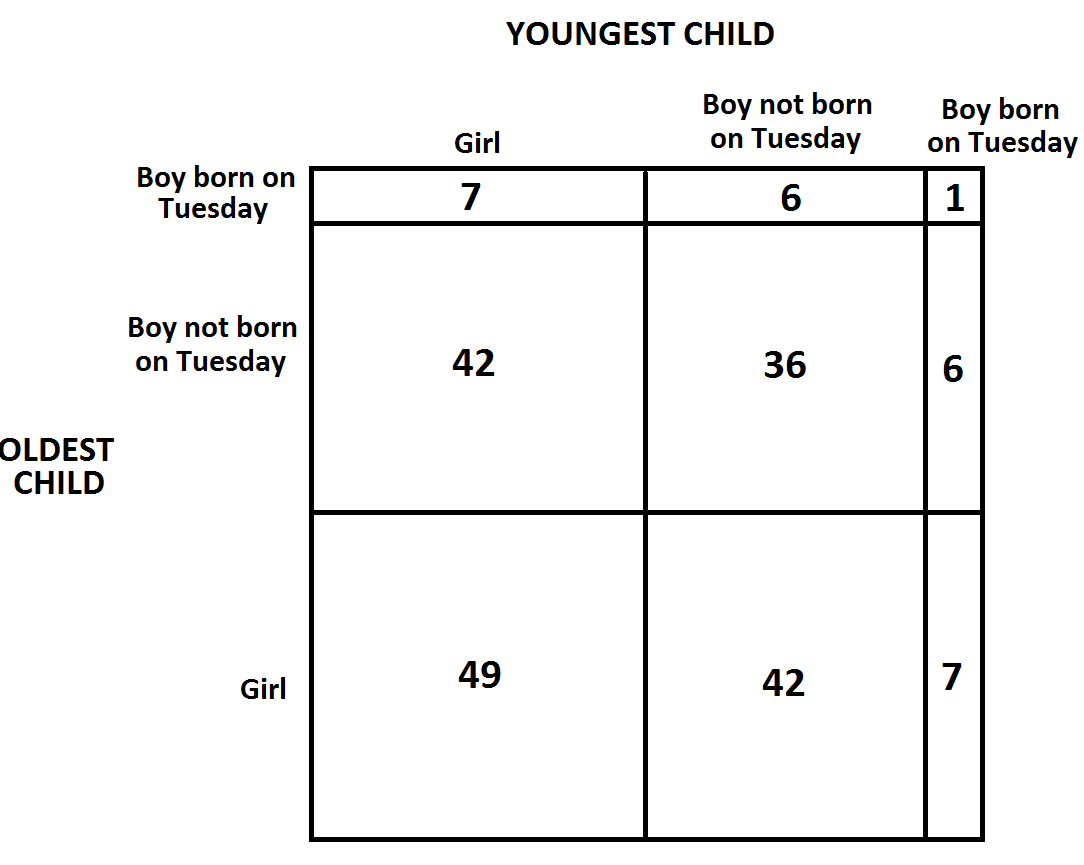
Again let’s follow the assumption that Cuthbert chose one of his children at random to comment on (each equally likely to be selected, again, a coin flip). Look at the table.

Of the \(7+6+7+6=26\) men with just one boy born on a Tuesday, half, that is, 13 will say “one of my children is a boy born on a Tuesday” after the flip of a coin. And the one man with two such boys will say this for certain. Of the 14 men who make this statement, \(\dfrac{1}{2}\left(6+6\right)+1=7\) of them have two boys. The chances that Cuthbert has two boys is thus 50%.

The chances that each man’s other child is a boy is 50% in each case, as people hearing the puzzle for the first time might expect (but for less subtle reasons!)

Exercise: Suppose we are now told that Bilbert and Cuthbert did not flip a coin to determine which child’s gender (and birthday) to reveal but come from a society in which one must mention that one of your children is a boy if you can, and better yet, must mention that you have a male child born on a Tuesday if you can legitimately do so.

Show that the probability that Bilbert has two boys is now \(\dfrac{1}{3}\) and the probability that Cuthbert has two boys is \(\dfrac{13}{27}\).

Often when this boy-boy puzzle is asked, no information is given as to what mechanism makes a gentleman decide to reveal that one of his children is male, and, as such, the problem is ill-defined and cannot be answered. This is the piece that snags even the most clever of minds.

To see what I mean, answer this much easier version of the puzzle. It really does show that assumptions about what makes people say what they do utterly affect answers.

Exercise: Suppose you know that Bilbert and Cuthbert come from a society that, if they have at least one daughter, would force them to say this. Given what they tell you in the original puzzle, what now are the chances they each have a male second child?

Do you see that the answer is now 100% each and every time?