Exploding Dots
2.4 We Speak \(1 \leftarrow 10\) Machine
As we saw in the video two lessons ago we are also set to explain the meaning of the \(1 \leftarrow 10\) machine.
For the \(1 \leftarrow 10\) machine we see that ten \(1\)s make \(10\), then ten \(10\)s make \(100\), ten \(100\)s makes \(1000\), and so on. A \(1 \leftarrow 10\) machine has ones, tens, hundreds, thousands, and so on, as dot values.
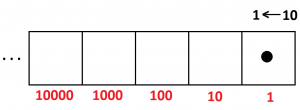
We saw that the code for the number \(273\) in a \(1 \leftarrow 10\) machine is \(273\), and this is absolutely correct: \(273\) is two hundreds, seven tens, and three ones.

In fact, we even speak the language of a \(1 \leftarrow 10\) machine. When we write \(273\) in words, we write
![]()
We literally say, in English at least, two HUNDREDS and seven TENS (that “ty” is short for “ten”) and three.
So, through this untrue story of dots and boxes we have discovered place-value and number bases: base two, base three, base ten, and so on. And society has decided to speak the language of base ten machine.
Why do you think we humans have a predilection for the \(1 \leftarrow 10\) machine? Why do we like the number ten for counting?
One answer could be because of our human physiology: we are born with ten digits on our hands. Many historians do believe this could well be the reason why we humans have favored base ten.
6. I happen to know that Martians have six fingers on each of two hands. What base do you think they might use in their society?
There are some cultures on this planet that have used base twenty. Why might they have chosen that number do you think?
In fact there are vestiges of base twenty thinking in western European culture of today. For example, in French, the number \(87\) is spoken and written as quatre-vingt-sept, which translates, word for word, as “four twenties seven.” In the U.S. the famous Gettysburg address begins: “Four score and seven years ago.” That’s four-twenties and seven years ago.
All right. The point of today’s lesson has been made. We have discovered base-ten place value for writing numbers and seen their context in the whole story of place value. We humans happen to like base-ten in particular because that is the number of fingers most of us seem to have.
In the next chapter we’ll start doing arithmetic with numbers, but in new and fabulous ways!
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


