We’ll now put some of our geometry results to good use. Our goal is to establish this next strange and curious fact.

Ride your bicycle in a large loop, starting in one position and ending in the same position. If you do this over sand or through snow or if your tires are dusty or wet, each tire will leave a track on the ground.

No matter which loop you choose to ride, the area between the two tracks is sure to be \(\pi r^2\)  where \(r\) is the distance between the two axles of the wheels.

You cannot escape and area of \(\pi r^2\)!

Whoa!

Roll your bicycle out of your garage in the morning and roll it back to the same storing position in the evening. Then the amount of area you traversed between your front and back tires was \(\pi r^2\), no matter what loop you rode that day!

Double whoa!

There are a few caveats to this claim.

If front and back wheel tracks cross, then there will be regions of area inside a given track and other regions outside of it. (In the sketch below, each grey region is inside the red track, for instance. If you choose to focus on the blue track, then each beige region lies inside it.) The total amounts of inside and outside areas are sure to differ by \( \pi r^2\)!

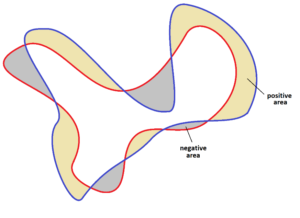
We’ve also implicitly assumed a “riding a loop” means that the path you trace has you conduct one full revolution of turning in total. But if you ride you bike around your house twice and then park it back in the garage (that is, you perform a “double loop”), then the area between your two tracks shall be \(2\pi r^2\). If you perform a triple loop, the area between the tracks shall be \(3 \pi r^2\), and so on. And if your tracks cross over as you ride, then you should regard some areas as positive area and others as negative area (like the grey and beige regions in the diagram above) and the total sum of areas in this case shall be \(\pi r^2\) or \(2 \pi r^2\) or \(3 \pi r^2\), and so on.

Also, if you follow a figure 8 (a forward loop and a backward loop adjoined), for instance, then the total area between your tracks shall be \( 1 \times \pi r^2 + \left(-1\right) \times \pi r^2 = 0\).

Let’s now work to these bold claims about area. Let’s study the mathematics of bicycle tracks next.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources