Once you’ve read this lesson, check out Levi’s video here for more explanation and practice! 

 

Here’s the division problem we are stuck on.

\(\dfrac{x^{3}-3x+2}{x+2}\)

 

And here is the picture for it again an \(1 \leftarrow x\) machine.

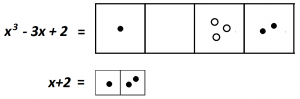
We are looking for copies of \(x+2\), one dot next to two dots, anywhere in the picture of \(x^{3}-3x+2\).  We don’t see any.

 

And we can’t unexplode dots to help us out as we don’t know the value of \(x\). (We don’t know how many dots to draw when we unexplode.)

 

The situation seems hopeless at present.

 

But I have a piece of advice for you, a general life lesson in fact. It’s this.

 

IF THERE IS SOMETHING IN LIFE YOU WANT, MAKE IT HAPPEN! (And deal with the consequences.)

 

Right now, is there anything in life we want?

 

Look at that single dot way at the left. Wouldn’t it be nice to have two dots in the box next to it to make a copy of \(x+2\)?

So let’s just put two dots into that empty box! That’s what I want, so let’s make it happen!

But there are consequences: that box is meant to be empty. And in order to keep it empty, we can put in two antidots as well!

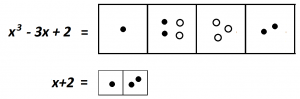
Brilliant!

 

We now have one copy of what we’re looking for.

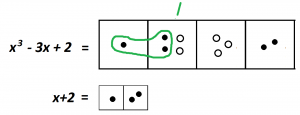
Is there anything else in life you want right now? Can you create another copy of \(x+2\) anywhere?

 

I’d personally like a dot to the left of the pair dots in the rightmost box. I am going to make it happen! I am going to insert a dot and antidot pair. Doing do finds me another copy of \(x+2\).

 

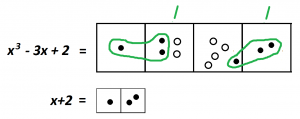
This is all well and good, but are we now stuck? Maybe this brilliant idea wasn’t actually helpful in the end.

 

Stare at this picture for a while. Do you notice anything?

 

Look closely and we start to see copies of the exact opposite of what we’re looking for! Instead of one dot next to two dots, there are copies of one antidot next to two antidots.

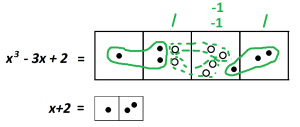
Whoa!

 

And how do we read the answer? We see that \(\left(x^{3}-3x+2\right)\div\left(x+2\right)\) is \(2x^2-2x+1\).

 

Fabulous!

 

So actually I was lying about fooling you. We can actually do all polynomial division problems with this dots and boxes method, even ones with negative numbers!

 

 

If you are looking for some practice problems, feel free to try these. Try them with pencil and paper, and then with the app perhaps. Answers, as usual, are in the final section of this chapter.

 

4. Compute \(\dfrac{x^{3}-3x^2+3x-1}{x-1}\).

5. Try \(\dfrac{4x^{3}-14x^2+14x=3}{2x-3}\).

6. If you can do this problem, \(\dfrac{4x^{5}-2x^{4}+7x^{3}-4x^{2}+6x-1}{x^2-x+1}\), you can probably do any problem!

7. This one is crazy fun: \(\dfrac{x^{10}-1}{x-1}\).

 

Aside: Is there a way to conduct the dots and boxes approach with ease on paper? Rather than draw boxes and dots, can one work with tables of numbers that keep track of coefficients? (The word synthetic is often used for algorithms one creates that are a step or two removed from that actual process at hand.)

 

Resources