Who said we need to stay with a \(1 \leftarrow 10\) machine?

The following picture shows that \(1432 \div 13 = 110 \; R2\) in a \(1 \leftarrow 5\) machine.

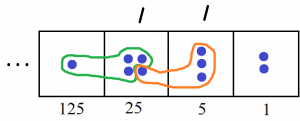
If we work with reciprocals of powers of five we can keep unexploding dots and continue the division process.

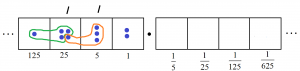
Here goes!

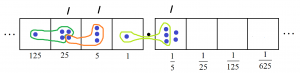
(This reads as \(1432 \div 13=110.1 \; R0.2\)  if you like.)

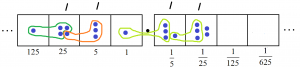
(This reads as \(1432 \div 13=110.11 \; R0.02\) if you like.)

And so on. We get, as a statement of base \(5\) arithmetic,

\(1432 \div 13=110.111\cdots\).

To translate this to ordinary arithmetic we have that

\(1432\) in base five is \(1 \times 125 + 4 \times 25 + 3 \times 5 + 1 \times 1 = 242\),

\(13\) in base five is \(1 \times 5 + 3 \times 1 = 8\),

\(110.111\cdots\) in base five is  \(30 + \dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\cdots\),

so we are claiming, in ordinary arithmetic, that

\(242 \div 8 = 30 + \dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\cdots\).

Whoa!

Question: What does the geometric series formula from chapter 7 say about the sum \(\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\cdots\)? Does it equal a quarter? (To be clear, in chapter 7 we showed that

\(1+x+x^2+x^3+\cdots = \dfrac{1}{1-x}\).

Multiplying through by \(x\) then gives

\(x+x^2+x^3+x^4+\cdots = \dfrac{x}{1-x}\).

Perhaps it is this second version of the geometric formula we need to work with now.)

Here are some (challenging) practice questions if you are up for them.

28. Compute \(8 \div 3\) in a base \(10\) machine and show that it yields the answer \(2.666\cdots\).

29. Compute \(1 \div 11\) as a problem in base \(3\) and show that it yields the answer \(0.02020202\cdots\). (In base three, “\(11\)” is the number four, and so this question establishes that the fraction \(\dfrac{1}{4}\) written in base three is \(0.020202\cdots\).)

30. Show that the fraction \(\dfrac{2}{5}\), written here in base ten, has the “decimal” representation \(0.121212\cdots\) in base four. (That is, compute \(2 \div 5\) in a \(1 \leftarrow 4\) machine.)

31. CHALLENGE: What fraction has decimal expansion \(0.3333\cdots\) in base \(7\)? Is it possible to answer this question by calling this number \(x\)  and multiplying both sides by \(10\)? (Does “\(10\)” represent ten?)

32. Use an \(1 \leftarrow x\) machine and \(x\)-mals to show that \(\dfrac{1}{x-1}=\dfrac{1}{x}+\dfrac{1}{x^2}+\dfrac{1}{x^3}+\dfrac{1}{x^4}+\cdots\).

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources