See how Goldfish and Robin, “Kids explain math to kids,” work to answer the question below for a \(1 \leftarrow 2\) machine: Thinking Video part 1 and Thinking Video part 2.

Throughout these notes we’ve hinted at the question as to whether or not results can change if we conduct dot explosions in a machine in different orders. It’s time to settle this question.

Prove that the order in which one conducts explosions in a \(1 \leftarrow 10\) machine without decimals (or for any \(A \leftarrow B\) machine, for that matter), does not matter. That is, for a given number of dots placed into the machine, the total number of explosions that occur will always be the same and the final distribution of dots will always be the same, no matter the order in which on chooses to conduct those explosions.

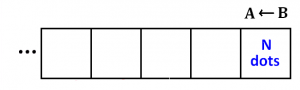
Hint: The total number of dots in the rightmost box is fixed and so the total number of explosions that occur there is fixed too. This means that the total number of dots that ever appear in the second box are fixed too, and so the total number of explosions that occur there is pre-ordained as well. And so on.

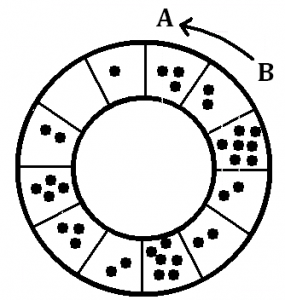
Question: The proof I outlined relies on there being a right boundary to the machine. If machines were circular, then matters are different. It would be worth playing with this! (When can we be certain that dots will eventually land in a stable distribution?)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources