We said in lesson 1.2 that one full turn, two full turns, in fact, any count of full turns, has the same final effect as no turning at all.

This is not true in some contexts! Try the following experiment.

Hold a teacup up in the air in the center of a room and have some friends tape four or five strings from the cup to various points about the room. Be sure to leave plenty of slack in the strings.

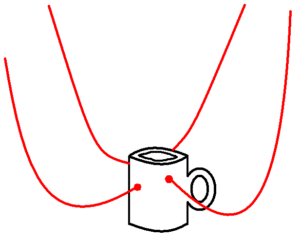
Rotate the teacup through one full turn, \(360^{\circ}\), tangling the strings in the process. (The handle serves as a pointer so that you can see when you have completed the turn.)

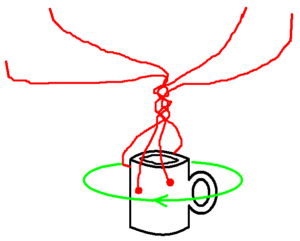
Now the cup is to be held fixed in space, never to move again!

You and your friends’ job now is to maneuver the strings up and under and around the cup and untangle them. (Whoever is holding the cup may have to move their hands out of the way, switch hands, and the like, but the cup itself is not to move.)

Can you untangle the strings?

Try as you might you will not succeed.

But let’s make matters worse!

Give the cup another full turn IN THE SAME DIRECTION (\(720^{\circ}\)), tangling the strings even further. 

Holding the cup fixed in space, try again maneuvering the strings up and under and the around the cup. This time you will be able to untangle them!

Absolutely do try this! (Perhaps try the experiment with three strings if you find yourself overwhelmed by strings.)

It turns out the that the tangle of strings from one full turn is fundamentally non-trivial—they cannot be untangled—but the tangle from two full turns is trivial and is equivalent to no tangle at all. (In fact, all tangles that result from an even number of full turns are trivial.)

So in this context, one-full turn is fundamentally different from two full turns.

Look up the WAITER’S TRICK for another physical demonstration of this phenomenon.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources