Here’s a classic riddle.

One day a woman decides to take a three-mile walk. 

She starts by heading directly south for one mile, trotting along at a happy pace, admiring the sunshine and the wildlife.  Then she turns left  and heads directly east for one mile, all the while enjoying the smell of the sweet air and the glorious sights of nature around her.  Next, she turns left one more time, exactly , and heads directly north just for one more mile. Surprisingly, after this third one-mile stretch she finds herself back to where she started!

What color was the bear she saw on her walk?

What?! What an absurd question! Firstly, it is surely impossible to conduct the journey described and end up back to one’s starting point.

And, secondly, none of the information provided mentions a bear nor provides any hint of the color of one. This puzzle is unanswerable nonsense!

Or is it?

It turns out there is one place on Earth where one can walk a mile south, a mile east, a mile north and end up back to start, and where one might possibly see a bear. Start at the north pole!

(In which case, any bear seen must be a polar bear and hence white.)

Comment: There are actually infinitely many different places in the southern hemisphere too at which one can conduct the journey described. (Choose a circle that circumnavigates the south pole with perimeter one mile, or with perimeter half a mile, or with perimeter one third of a mile, and so on. Now start the your three-mile journey one mile north of the circle you identify.) But as there are no bears in the Antarctic, the riddle cannot be set there. We must be in the northern hemisphere.

Let’s extend the woman’s walk. Suppose now she walks from the north pole south all the way down to the equator, then turns \(90^{\circ}\) east and walks an equal distance along the equator, to then turn \(90^{\circ}\) to head back to the north pole. This creates a large triangle with three \(90^{\circ}\) turns.

Notice that the angles in this triangle sum to \(270^{\circ}\) , not \(180^{\circ}\) !

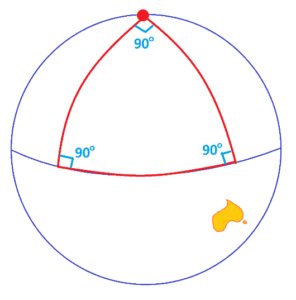
But here’s the kicker. 

Pencil pushing still works in this triangle and insists that the three angles of the triangle sum to \(180^{\circ}\) , half a turn!

Imagine you walk the path of this big triangle, starting at the north pole and pushing a pencil straight in front of you towards the equator. When you reach the equator, rotate the pencil to point east. After pushing the pencil straight along the equator, you then turn it north. Next, you push the pencil straight north until you come back to the north pole, and then rotate the pencil through this third angle. Can you see in your mind’s eye that if you could actually perform this experiment that the pencil will be back in its original alignment but facing the opposite direction, just as though it had undergone a 180-degree rotation?

What’s going on?

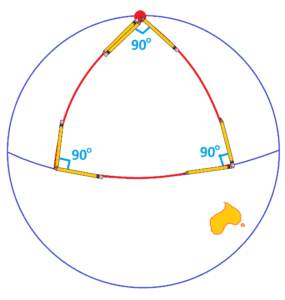
Of course, you might well argue that this example does not apply because the Earth is not flat and the lines along which we are pushing the pencil are not straight. Fair enough. But then why are we willing to believe that the pencil trick is working properly for all the (small) triangles we are drawing on pieces of paper or on boards? How do we know the paper is flat? How do we know the board isn’t slightly warped? The pencil trick will always say that the angles in a “triangle” sum to \(180^{\circ}\) !

Question: Here is a “triangle” with sides that are clearly not straight. Can you see that pushing the pencil along the sides of this triangle, and rotating it at each corner, still produces a net effect of a \(180^{\circ}\)  turn on the pencil?

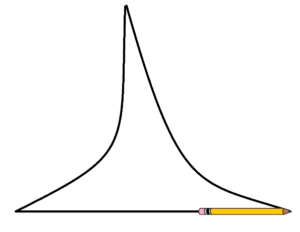
So maybe the pencil is only speaking truth when we are sure the sides of the figure we are working with are, for certain, straight. After all, we did say that sliding the pencil along the side of a figure does not apply any turning to it.

But that now begs the question: How do we know whether or not a path is straight? If I were to go outside and walk due south my path, I am sure, will feel straight to me. Someone observing from space might say my path is curved, but here in Earth I am not sure how I would know.

For a triangle drawn on the classroom floor we might feel that its sides are straight. For a triangle drawn on a soccer field we might feel that its sides are straight. If we draw a triangle the size of the state of Iowa, would we still feel that its sides are straight?

As I question pencil-pushing more and more, more questions and worries come to the fore. My brain is starting to hurt!

So how do we extract ourselves from unending philosophical pickles?

Let’s go back to what we like to believe.

In a theory of geometry we feel that there should be some notion of a line being “straight” and that we can make figures with segments of these straight lines. On a page of paper or on a chalkboard, which we like to believe is “flat,” we draw these lines with a ruler which we believe is straight. On the surface of the Earth, the line segments we feel are straight are different, they are sections of large circles, like a section of the equator. (These lines certainly feel “straight” when on the surface of the Earth.)

But these two geometries—geometry on paper and geometry on a sphere—will be different. We don’t think of the geometry on the surface of the Earth as “flat.”

And what is the difference we observed? It’s the nature of angles inside triangles.

So let’s turn all our confused and hazy thoughts into a definition and a statement of belief.

Definition: Call a geometry flat if we can be sure that the three interior angles of each and every triangle in the geometry have measures adding to \(180^{\circ}\) .

A Fundamental Assumption of Geometry:  We choose to believe that the geometry studied in school is flat.

There! Philosophical pickles resolved simply by being fully open and honest and declaring that we’re going to make a fundamental assumption about how our geometry shall work. Spherical geometry is not flat and shall work differently than the geometry we study in school, one that we presume is flat.

HISTORICAL COMMENT

The great Greek scholar Euclid (ca 300-260 BCE), hailed as the one of the greatest intellects of all time, is revered for his 13-volume series, The Elements. Here Euclid outlines the entire theory of geometry as based on a small set of fundamental beliefs and their logical consequences.  (Euclid starts with 10 basic beliefs, but later scholars realized Euclid implicitly made additional assumptions in his work. In the late 1800s German mathematician David Hilbert adjusted the list of Euclid’s beliefs to 28 axioms to produce a full set of initial beliefs needed for a logically complete theory of geometry.)

Euclid declared too, as one of his fundamental assumptions, a statement about “flatness.” He chose a variant belief about triangles.

Euclid’s Fifth Postulate: If the two angles shown have measures summing to less than a half turn, then the two blue lines shown, if extended, will meet to form a triangle.

Euclid then used this assumption (and his other assumptions) to logically deduce that the measures of the three interior angles of any triangle sum to \(180^{\circ}\) . But it is also possible to start with our fundamental belief about angles in a triangle and deduce Euclid’s Fifth Postulate from it (and the remaining basic assumptions). Thus, these two different fundamental beliefs about triangles are logically equivalent beginning assumptions to geometry.

The geometry studied in school textbooks, our “flat geometry,” is usually called Euclidean geometry.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources