Global Math Project Experiences
1.7 Pencil-Pushing Inspires Truth Nonetheless
Lesson materials located below the video overview.
We are now assuming that geometry is flat, that is, that angles in triangles are sure to have measures that sum to half a turn. In other words, we are simply choosing to believe what pencil pushing says about angles in triangles.
Does this mean that what the pencil says about angles for other shapes might be true too in flat geometry?
Example: Back in lesson 1.2 pencil pushing suggested that the four angles in this quadrilateral have measures that sum to \(360^{\circ}\). Is this true in flat geometry?
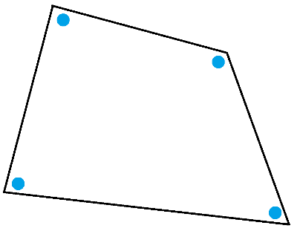
Answer: Yes, it is! Divide the quadrilateral into two triangles as shown. By our flatness belief, the measures of the three green angles sum to \(180^{\circ}\), as do the measures of the three orange angles. And the sum of all six angles, which is \(360^{\circ}\), matches the sum of the four original blue angles in the quadrilateral.
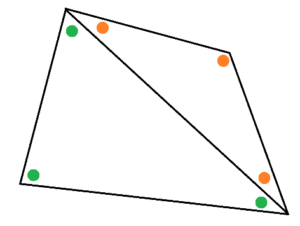
| Question 1: Show, in flat geometry, that the sum of the measures of the interior angles of this next quadrilateral do indeed sum to \(360^{\circ}\).
Question 2: Do you feel it is true that every 5-sided polygon subdivides into three triangles? If so, what does this say is the sum of the measures of the interior angles of a five-sided polygon?
Question 3: Do you feel it is true that every 13-sided polygon subdivides into eleven triangles? If so, what does this say is the sum of the measures of the interior angles of a 13-sided polygon? What general formula might you suggest for the sum of measures of the interior angles of a polygon with \(N\) sides?
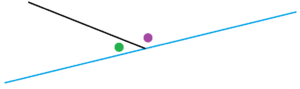
Question 4: The beginning assumptions in the theory of geometry show that for any straight line, such as the one shown in blue, with two angles constructed on it as shown have measures summing to \(180^{\circ}\). (This feels intuitively correct!)
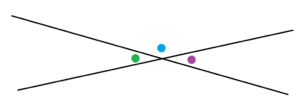
a) Use this next diagram to show that pencil-pushing is correct in suggesting that vertical angles must have the same measure. (Explain why the green and the purple angles have the same measure.)
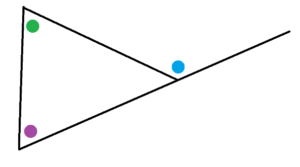
b) Explain why the sum of the measures of the green and the purple angles in this diagram equals e measure of the blue angle.
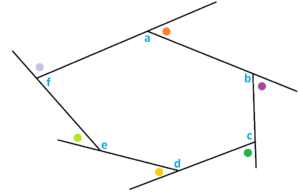
c) A hexagon subdivides into four triangles and so the measures of its six interior angles sum to \(4 \times 180^{\circ}\). In this diagram where these measures are denoted \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\) and we have \(a+b+c+d+e+f=4 \times 180^{\circ}\).
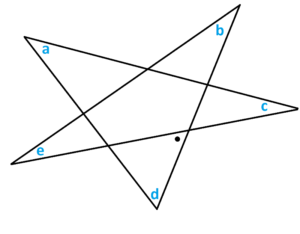
Use this to show that pencil pushing was correct to say that the six exterior angles (shown as dots) have measures that sum to \(360^{\circ}\). d) CHALLENGE: Show that pencil-pushing was correct to say that the measures of the angles shown in a lopsided star (represented as letters) add to half a turn, that is, \(a+b+c+d+e=180^{\circ}\). (Hint: Why is the measure of the angle with the dot equal to \(b+e\)?)
|
It seems we can use pencil-pushing nonetheless to guide us to possible true statements in flat geometry.
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()