Let’s do a “deep dive” into special sequences of numbers.

 

If you do believe that patterns likely hold true, what then would you say is the next number in this sequence?

No doubt you noticed the constant difference of 3 between the terms we see and so would guess the next entry to be 20. Of course there is no reason to believe that all differences will forever remain constant, but noticing this for what we have makes 20 an intelligent guess for the next number.

Of course not all sequences have constant differences. For example, this sequence fails to have a constant difference between terms.

But it does have constant “second differences.”

A sequence like this one,  17  17  17  17  17  17  17  17 …,  is constant from the start.

 

Practice 1: Make an intelligent guess as to the next number in the sequence : 2  3  6  11  18  27  38  __.

 

Practice 2: Consider the following sequence of diagrams each made of squares 1 unit wide.

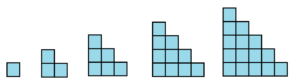
If the implied geometric pattern from these first five figures continues …

a) What would the perimeter of the tenth figure likely be?

b) What would the area of the tenth figure likely be?

 

Practice 3:

a) Show that for the following sequence it seems that the third differences are constant. Make a prediction for the next number in the sequence.

0  2  20  72  176  350  612 …

 b) How many differences must one complete in the sequence below to see a row of constant differences? (The sequence is the powers of two.)

1  2  4  8  16  32  64  128  256  …

 

Practice 4:

a) The sequence of square numbers begins 1, 4, 9, 16, 25, 36, 49, 64, …. (The \(n\)th number in this sequence is \(n^2\).)

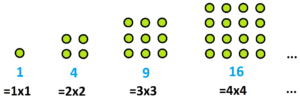
Is there a row in the difference table of the square numbers that is constant?

b) The sequence of cube numbers begins 1, 8, 27, 64, 125, 216, 343, 256, …. (The \(n\)th number in this sequence is \(n^3\).)  Is there a row in the difference table of the cube numbers that is constant?

 

Practice 5: Use differences to make an intelligent guess as to the next element of this sequence.

             -1   4   7   8   7   4   -1   __

 

LEADING DIAGONALS

Here is a sequence and a table of all its differences! (Well, if we trust patterns, it is clear that the difference rows are eventually all zero.)

The first entry in each difference row form the leading diagonal of the difference table.

 

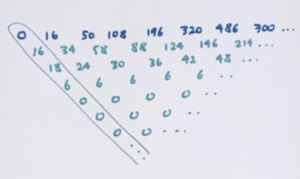
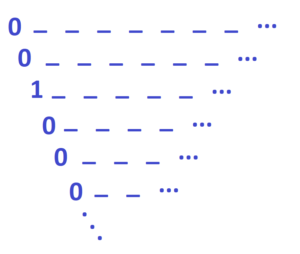
And here now is just a leading diagonal of some difference table. Check that you can construct the original sequence from it. For example, the second entry on the top row must differ from 1 by zero, and so also be 1. The second entry on the second row must differ from 0 by two, and so be 2. This means that the third entry on the top row must be 3. (Do you see why?) And so on.

Practice 6: Do this! Show that you can fill in the entire set of blanks in a difference table just from knowing the table’s leading diagonal.

 

Practice 7: What sequence has 0  0  1  0  0  0  0  0  0  … as its leading diagonal?

 

We learn

To know the leading diagonal of a difference table is to know the original sequence! 

 

So let’s now get to know some leading diagonals of sequences.

 

GETTING FORMULAS FROM LEADING DIAGONALS

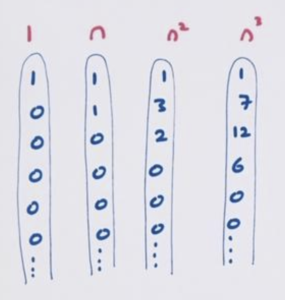
Here’s the constant sequence of 1s and its leading diagonal. The \(n\)th term of this sequence is, well, 1!

And here’s the sequence of counting numbers and its leading diagonal. The \(n\)th term of this sequence is \(n\).

A previous practice question looked at the sequences of square numbers (with \(n\)th term given by \(n^2\)) and cube numbers (with \(n\)th term given by \(n^3\)). Here are their leading diagonals.

Optional: Care to work out the leading diagonal for the sequence of fourth powers too? (Here the \(n\)th term of the sequence is given by \(n^4\).) The answer could be no!

 

Now consider this.

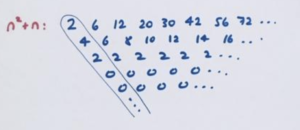
Look at the sequence with \(n\)th term given by \(n^2+n\).

The first term of the sequence is \(1^2+1=2\), the second term is \(2^2+2=6\), the third term is \(3^2+3\), and so on. We get sequence 2, 6, 12, 20, 30, 42, ….     

Is the leading diagonal of this sequence just the sum of the diagonals for the sequences given by \(n^2\)  and \(n\) (adding matching entries in each diagonal, perhaps)?

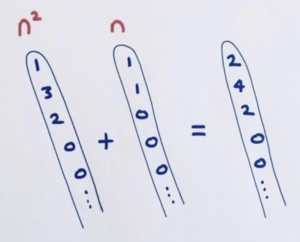
Let’s check.

Here’s the difference table for the sequence given by \(n^2+n\).

Yes! Its leading diagonal is indeed the sum of the diagonals for \(n^2\) and for \(n\). Wow!

 

Comment: I am getting a bit loose with my language. Instead of saying “the leading diagonal for the sequence with \(n\)th term given by \(n^2\), ” for instance, I am just saying “the leading diagonal for \(n^2\).” I hope my short-hand language is clear enough.

 

This example suggests a strategy for finding formulas for sequences from our catalogue of standard leading diagonals.

When given a sequence of integers

1. Find its leading diagonal by constructing its difference table.

2. Try to recognize that leading diagonal as a combination of standard leading diagonals.

     This will give a candidate formula for the sequence.

This is, of course, assuming we trust patterns and choose to believe that everything just hangs together beautifully and magically. But since we are only dealing with a finite number of terms of any sequence, we can always check our potential formula by plugging in values for \(n\) and seeing if does indeed produce that desired list of numbers. We need a third step.

3. Check to see if the candidate formula actually works.

 For the record, here again are our standard leading diagonals.

(Feel free to add to this picture the diagonals for the fourth, fifth, sixth, … powers too!)

 

Example: Find a formula for the sequence : 1   6   15   28   45   66   …

(This is, of course, under the assumption we can trust patterns.)

 

Answer: Here is the difference table for the sequence and its leading diagonal (assuming we can trust the pattern of zeros continues).

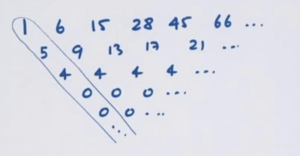
Is this leading diagonal some combination of our standard diagonals?

Notice that our leading diagonal has 0s in the fourth position onwards. This tells us we likely won’t need to use the diagonal for \(n^3\) (or for any higher of  \(n\) if you tried working out the diagonals for the fourth powers and the like) as it has non-zero terms in those positions.

So let’s focus on using the diagonals of \(1\) and \(n\) and \(n^2\).

Our leading diagonal has the number 4 in the third position and only the diagonal \(n^2\) has a non-zero entry in the third position. It looks like we’ll need two copies of \(n^2\).

We need 5 in the second position and right now we have double 3, to give 6, in that position. This shows we need -1 copies of the \(n\) diagonal.

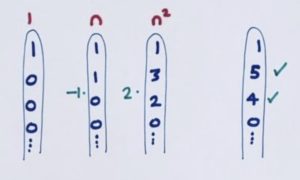
The 4 and the 5 in the target diagonal are now all set, and so is the beginning 1 by luck. We don’t need the \(1\) diagonal at all.

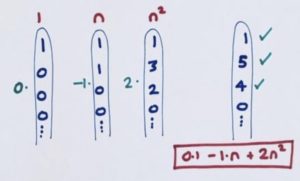
So our candidate formula for the sequence is \(2n^2-n\). And putting in 1, 2, 3, 4, 5, and 6 for \(n\) in turn confirms this formula gives the outputs 1, 6, 15, 28, 45, and 66.

We have found a formula for the sequence!

 

Practice 8: Use difference methods to find a formula for the sequence of numbers: 2, 2, 4, 8, 14, 22, 32, …

(Just so you know, the answer is \(n^2-3n+4\). Can you see get this from looking at the leading diagonal for the sequence?)

 

Practice 9:  Find a formula that fits the sequence 0, 2, 10, 30, 68, 130, 222, ….

(The answer is \(n^3-3n^2+4n-1\).)

 

Practice 10:

a) Find a formula that fits the sequence 5, 8, 11, 14, 17, 20, 23, ….

b) Find a formula that fits the sequence 3, 3, 3, 3, 3, 3, 3, ….

c) Find a formula that fits the sequence 1, 3, 15, 43, 93, 171, 283, ….

d) Find a formula that fits the sequence 1, 0, 1, 10, 33, 76, 145, 246, 385, ….

e) Find formulae for as many of these sequences you feel like doing!

3  3  7  21  51  103  183  297  ...

0  9  24  45  72  105  144  189  240  …

6  24  60  120  210  336  …

230  275  324  377  434  495  …

 

Practice 11: Find a general formula for the th triangular number: 1, 3, 6, 10, 15, 21, 28, 36, ….

(Don’t be afraid of fractions!)

 

Practice 12: Let \(S\left(n\right)\) be the total number of squares, of any size, one can find in an \(n\times n\) grid of squares. For example, \(S\left(3\right) = 14\) because one can find nine \(1 \times 1\) squares, four \(2 \times 2\) squares, and one \(3 \times 3\) square, for a total of \(9+4+1=14\)  squares in a  grid.

a) Find \(S\left(1\right)\), \(S\left(2\right)\), \(S\left(4\right)\), and \(S\left(5\right)\).

b) What do our general difference methods suggest for a general formula for \(S\left(n\right)\)?

c) OPTIONAL CHALLENGE: What is the value of \(1^2+2^2+3^2+ \cdots +99^2 + 100^2\)?    

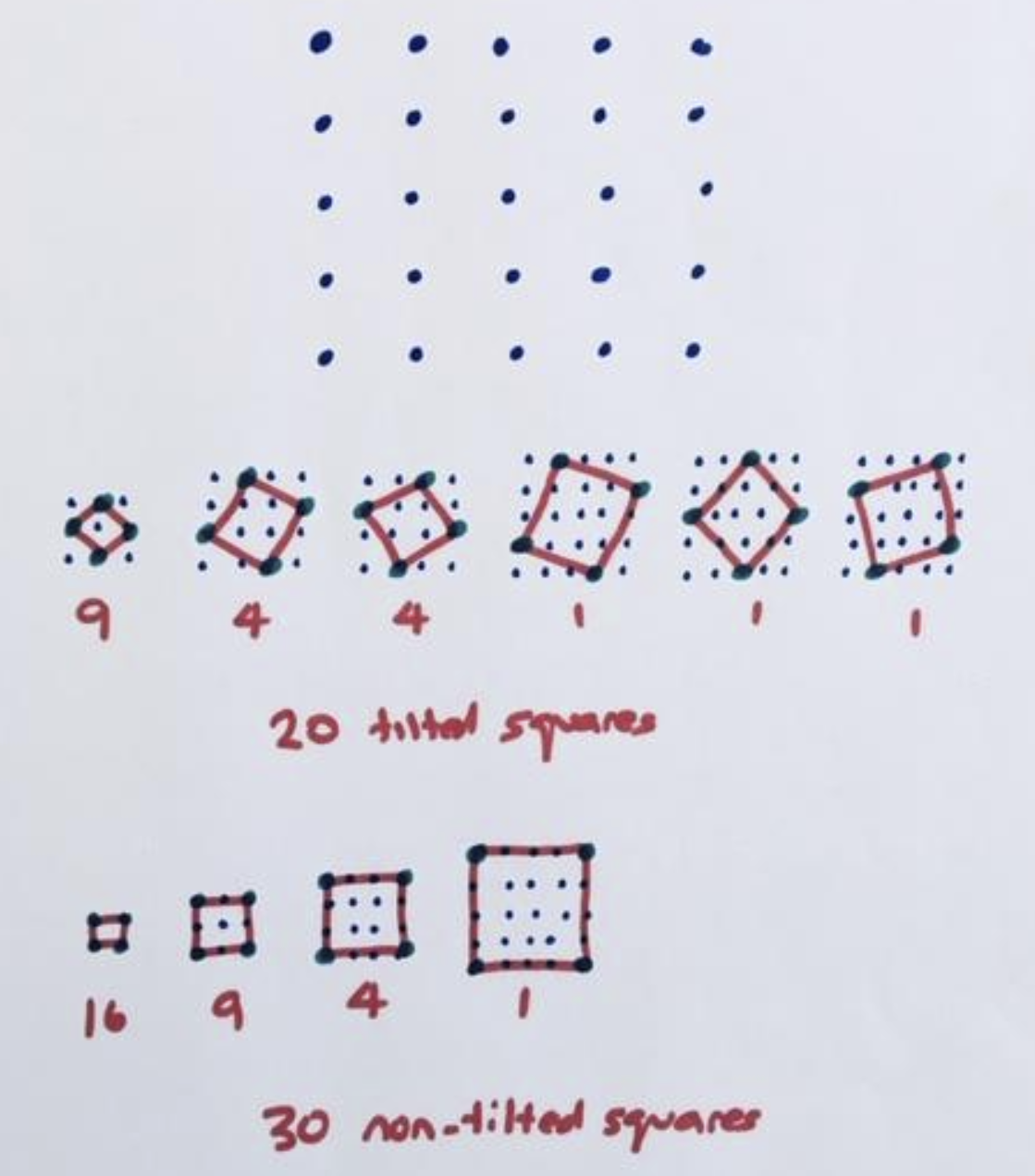
d) OPTIONAL CHALLENGE: Care to count titled and non-tilted squares on arrays?

For instance, on a five-by-five array of dots on can draw 30 non-tilted squares and 20 titled squares giving 50 squares in total.

 

BUT WE CAN’T TRUST PATTERNS!

Here’s one of my favourite puzzles.

 

Draw some circles with dots on their boundaries: one with 1 dot on its boundary, one with 2 dots on its boundary, one with 3 dots on its boundary, and so on.

Next, for each circle, connect each and every pair of boundary dots with a line segment. This divides each circle into a number of regions. Count the regions.

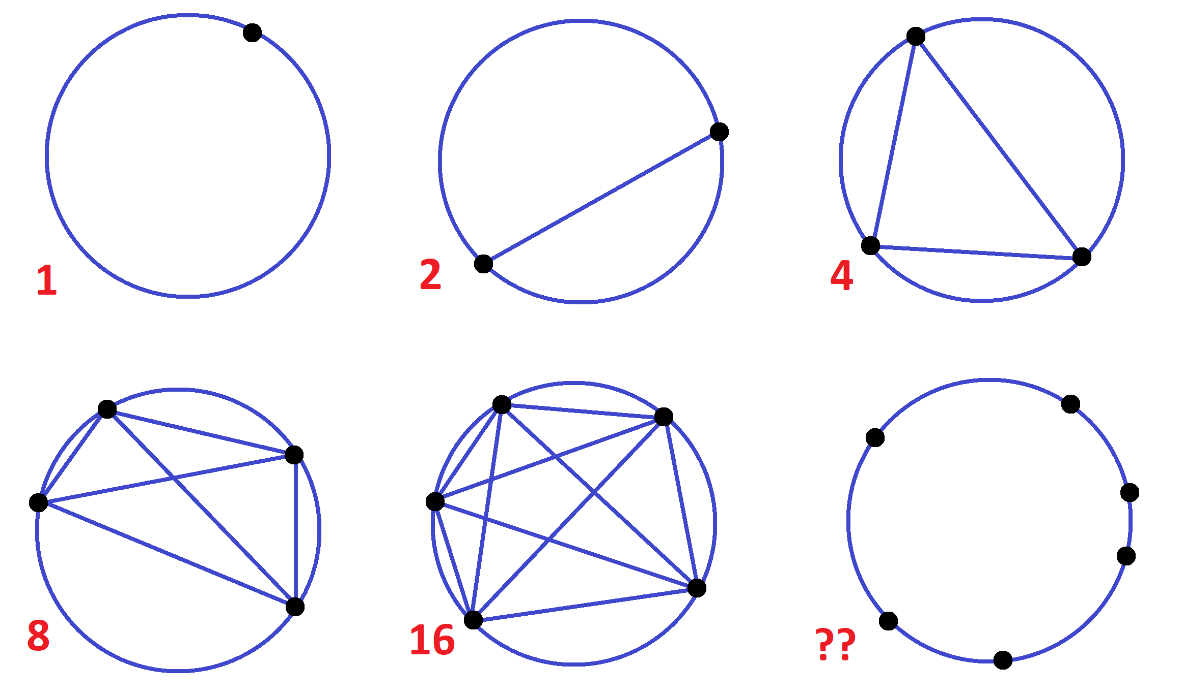
The circle with one dots has 1 region. The circle with two dots, 2 regions. The circle with three dots, 4 regions. The circle with four dots, 8 regions. The circle with five dots, 16 regions.

How many pieces do you expect to see from six boundary dots?

 

Up to now we’ve been trusting patterns, and our trust clearly says to expect 32 regions to appear from connecting six dots. (The count seems to double every time.)

 

But try as you might, you will not get 32 pieces!

 

Try it! You will either see 30 or 31 regions depending on how you place your dots. (If you are a person who likes to space one’s dots symmetrically about the boundary, for instance, you will see only 30 pieces. You will create a multiple intersection point that masks an extra region.)

So here is the moral of this puzzle.

We cannot trust patterns!

We can be excited by patterns. We can be motivated by patterns. But we can never trust a pattern until we have a logical reason to justify why it should be true.

People sometimes say that mathematics is about finding patterns. That is not quite right. It is about finding patterns and structure AND THEN using logical reasoning to explain why those patterns are true and that structure holds—or to find counter examples to show that one’s suspicions are wrong.

 

CHALLENGE: Suppose 7 dots are placed on the boundary of a circle in such a manner that the maximal number of regions result when one connects pairs of dots with line segments. How many regions is that?

What is the maximal number of regions that can result with 8 dots? With 9 dots?

Care to keep computing more and more terms of our sequence?

1   2   4   8   16   31  __  __  __  __  __ …

 

 

ULTRA-CHALLENGE: Might there still be a formula for the numbers in this sequence?

Comment: See chapter 4 of MATH GALORE! (MAA, 2012). High-school students found such a formula and proved it works!

 

Resources