We have now seen that not all curves that appear to be quadratic actually are!

Let’s see what we can do now if we don’t trust the patterns we see in sequences.

 

Suppose you take an intelligence test and are asked this question.

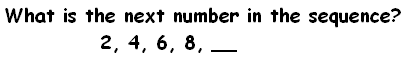
Clearly you would answer \(17\), because you could see that this sequence is following the formula

\(\dfrac{7}{24}n^4-\dfrac{35}{12}n^3+\dfrac{245}{24}n^2-\dfrac{151}{12}n+7\).

(Test this. Put in \(n=1\) and see the formula gives 2. Put in \(n=2\) and see it gives 4, put in \(n=3\) to see it gives 6, put in \(n=4\) to see it gives 8, and finally, put in \(n=5\) to see it gives 17.)

 

Actually, you change your mind, and say the next number is \(-8\) because you recognize the sequence as following the formula

\(-0.75n^4+7.5n^3-26.25n^2+39.5n-18\).

(Test this. Put in \(n=1\) and see the formula gives 2. Put in \(n=2\) and see it gives 4, put in \(n=3\) to see it gives 6, put in \(n=4\) to see it gives 8, and finally, put in \(n=5\) to see it gives \(-8\).)

 

But then you realize that you can write down any number for the next value, and so you decide to just answer with the symbol \(A\) for a general number knowing that

\(\dfrac{(A-10)}{24}\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)+2n\)

gives the value 2 for  \(n=1\), 4 for  \(n=2\), 6 for \(n=3\), 8 for \(n=4\), and \(A\) for \(n=5\).

 

The fact is one can readily create a formula to fit any finite set of data values, including a data set that has a “crazy” final term.

This shows that believing in patterns can be dangerous!

 

So how does one find formulas to fit data?

 

We give two methods.

Our first technique for finding formulae for data is due to French mathematician Joseph-Louis Lagrange (1736-1813) and is today called Lagrange’s Interpolation Formula. It looks shockingly scary at first.

 

Lagrange’s Interpolation Formula Here is an “obvious” formula that takes the values \(A\), \(B\), \(C\),  \(D\), and \(E\) for the values \(n=1\), \(2\), \(3\), \(4\), and \(5\) in turn.   \(A\dfrac{\left(n-2\right)\left(n-3\right)\left(n-4\right)\left(n-5\right)}{\left(-1\right)\left(-2\right)\left(-3\right)\left(-4\right)}+B\dfrac{\left(n-1\right)\left(n-3\right)\left(n-4\right)\left(n-5\right)}{\left(1\right)\left(-1\right)\left(-2\right)\left(-3\right)}+C\dfrac{\left(n-1\right)\left(n-2\right)\left(n-4\right)\left(n-5\right)}{\left(2\right)\left(1\right)\left(-1\right)\left(-2\right)}+D\dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-5\right)}{\left(3\right)\left(2\right)\left(1\right)\left(-1\right)}+E\dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)}{\left(4\right)\left(3\right)\left(2\right)\left(1\right)}\)

 

Indeed, this looks horrific at first glance! But actually it is easy to understand after one has taken a deep breath.

Let’s process it in stages.

 

1. First note that there are five terms added together.

2. There is one term for each appearance of the values \(A\), \(B\), \(C\), \(D\), and \(E\).

3. Each term is designed to vanish for all but one of the values \(n=1\), \(2\), \(3\), \(4\), and \(5\).

 

To make sense of this third statement, put \(n=1\), say, into the formula and see what it does to each term of in the expression. For example, the second term is \(B\dfrac{\left(n-1\right)\left(n-3\right)\left(n-4\right)\left(n-5\right)}{\left(1\right)\left(-1\right)\left(-2\right)\left(-3\right)}\) with the factor \(\left(n-1\right)\) in its numerator. When we put \(n=1\) into this expression we thus get zero in the numerator of the expression and thus the whole expression equals zero.

The third, fourth, and fifth terms in the sum also have a factor of \(n-1\) in their numerators, and so each equal zero when \(n\) equals \(1\).

Only the first term will be non-zero for \(n=1\).

 

Check: Put \(n=4\) into the formula. Which terms vanish for \(n=4\)? Which one term “survives” for \(n=4\)?

 

4. Each term in the sum is a number times a fraction. The fraction is designed to equal 1 at a specific value of \(n\).

 

To make sense of this, consider putting in \(n=1\) again. The final four terms in the sum are zero and only the first term “survives.” But look what happens when we put in \(n=1\) into the first term. We get

\(A\dfrac{\left(1-2\right)\left(1-3\right)\left(1-4\right)\left(1-5\right)}{\left(-1\right)\left(-2\right)\left(-3\right)\left(-4\right)}=A\times 1=A\).

The denominator was designed to match the numerator for this instance and the term has value \(A\). The sum of all five terms equals \(A+0+0+0+0=A\) for \(n=1\), just as wanted.

 

Check: Put \(n=4\) into the entire formula and see it gives the value \(0+0+0+D\times 1+0=D\), just as hoped.   

 

Practice 1: Convince yourself that the formula

\(8\dfrac{\left(n-10\right)\left(n-20\right)}{\left(-4\right)\left(-14\right)}+122\dfrac{\left(n-6\right)\left(n-20\right)}{\left(4\right)\left(-10\right)}+4600\dfrac{\left(n-6\right)\left(n-10\right)}{\left(14\right)\left(10\right)}\)

 gives the value 8 for \(n=6\), the value 122 for \(n=10\), and the value 4600 for \(n=20\).

 

Practice 2: Find a formula that gives the value \(9000\) for \(n=3\), the value \(-45\) for \(n=5\), and the value \(\dfrac{2}{3}\) for \(n=8\). (Don’t bother simplifying your formula.)

 

Practice 3: Write down a formula that fits this data set.

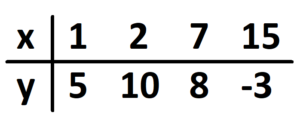
Practice 4: You are asked to write the next number in this sequence:                 

1   2   3   4   __

You decide to write \(\sqrt{\pi}\). Write down a formula that justifies your answer.

 

Pedagogical Comment: Many school curricula ask students to find a quadratic formula \(y=ax^2+bx+c\) to fit three data points. Lagrange’s Interpolation formula works very well for this. The task of simplifying the formula one gets (if one is required to simplify answers) is not too onerous.

 

Back to Difference Methods

Here’s a second method for finding formulae for finite data sets. It’s our earlier approach with difference methods.

Let’s go back to the very first sequence of this lesson. Let’s find a formula that fits the data

2  4  6  8  17.

To do so, just write out a difference table for those five data values and pretend that the final row is a line of constant differences.

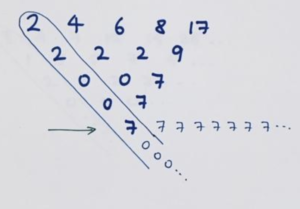
Look at the leading diagonal and recognize it as a combination of standard leading diagonals just as before. For example, using Newton’s insight of lesson 5 we get the formula

\(2 \cdot 1+ 2 \cdot \left(n-1\right) + 7 \cdot \dfrac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)}{24}\)

which matches the first formula I presented in this lesson.

 

Practice 5: Find an expression  \(an^2+bn+c\) that fits the sequence 5  6  10. (That is, find a formula that gives 5  for \(n=1\),  6 for \(n=2\), and 10 for \(n=3\).)

 

Resources