In the lessons about sequences I was very careful to point out that we were getting candidate formulas for our sequences and that we had to go to the trouble to check if they actually work. Well, it turns out that they will always work, and now we have the means to prove that they will.

The argument is theoretical, and I’ll demonstrate the gist of it here with one specific instance. We’ll prove:

If a sequence has a difference table with constant second differences (but not constant first differences), then than sequence is given by a formula of the form \(an^2+bn+c\), a quadratic formula. Moreover, this is the formula that arises by recognizing the leading diagonal as a combination of the \(1\), \(n\), and \(n^2\) leading diagonals.

The same approach can be used to prove:

If a sequence has a difference with constant third differences (but not constant second differences), then that sequence is given by a cubic formula \(an^3+bn^2+cn+d\).

 If a sequence has a difference with constant fourth differences (but not constant third differences), then that sequence is given by a quartic formula \(an^4+bn^3+cn^2+dn+e\).

And so on. We also have

If a sequence has a difference with constant differences (but the sequence itself is not constant), then that sequence is given by a linear formula \(an+b\).

Our very first example was an example of a “linear sequence”. It is generated by the formula \(3n-1\).

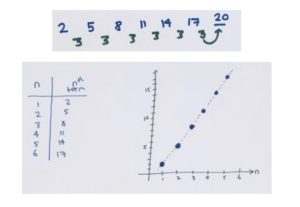
Let’s prove the claims made about a sequence with constant second differences.

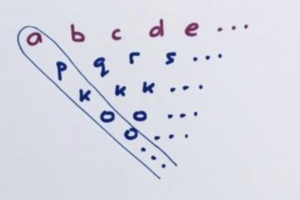
Suppose a  b  c  d  e  …  is such a sequence.

1. Lagrange’s interpolation formula shows that there is a quadratic expression that gives the value a for \(n=1\), b for \(n=2\), and c for \(n=3\).

\(a\dfrac{\left(n-2\right)\left(n-3\right)}{\left(-1\right)\left(-2\right)}+b\dfrac{\left(n-1\right)\left(n-3\right)}{\left(1\right)\left(-1\right)}+c\dfrac{\left(n-1\right)\left(n-2\right)}{\left(2\right)\left(1\right)}=An^2+Bn+C\)

2. This quadratic formula generates its own sequence and difference table. Since the first three terms of the first row were designed to match the original sequence, the first two terms of the second row and the first term of the third row of the difference table match the difference table of the original sequence too.

3. The difference tables of each of the sequences \(1\) and \(n\) and \(n^2\) is zero from the fourth row onwards, and it follows that the difference table for \(An^2+Bn+C\) must be zero as well beyond the third row.

4. Thus our original sequence and the sequence from the quadratic expression \(An^2+Bn+C\) have matching leading diagonals: a p k 0 0 0 … . This means that all terms of the two difference tables—including the entries of the first row, the two sequences—match.

We conclude: Our original sequence is generated by the formula \(An^2+Bn+C\).

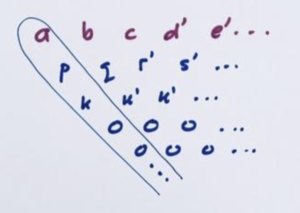
5. Could two different quadratic expressions \(An^2+Bn+C\) and \(A’n^2+B’n+C’\) generate the same sequence?

If this were possible, then their difference \(\left(A-A’\right)n^2 + \left(B-B’\right)n+\left(C-C’\right)\) would be an expression that gives only zero values, that is, produces a sequence that is all zeros. But if any of the values \(A-A’\), \(B-B’\), or \(C-C’\) is non-zero, this would not be the case. So it must be the case that \(A=A’\), \(B=B’\), and \(C=C’\).

We conclude: There is only one quadratic expression that generates a sequence with constant second differences.

So once you have found one quadratic expression that works, you have found the quadratic expression that works!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources