We have:

\(1! = 1\)

\(2! = 2 \times 1 = 2\)

\(3! = 3 \times 2 \times 1 = 6\)

\(4! = 4 \times 3 \times 2 \times 1 = 24\)

\(5! = 5 \times 4 \times  3 \times  2 \times  1 = 120\)

\(6! = 6 \times  5 \times  4 \times  3 \times  2 \times  1 = 720\)

\(7! = 7 \times 6 \times 5 \times 4 \times  3 \times  2 \times  1 = 5040\)

\(8! = 8 \times 7 \times 6 \times 5 \times 4 \times  3 \times  2 \times  1 = 40320\)

 A graph of these values appears as follows:

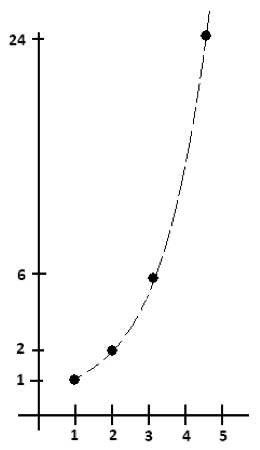
In 1729, at the age of 22, Swiss mathematician Leonhard Euler wondered if there is a formula for a general function that “connects the dots” of the factorial numbers. And he found one! He called it the Gamma Function. The curious thing is that one can input rational and irrational values into the Gamma function and obtain meaningful answers. The Gamma function gives \(1! = 1\) and \(0! = 1\)  (just as the mathematics we saw earlier suggests) and it also gives:

\(\left(\dfrac{1}{2}\right)! = \dfrac{\sqrt{\pi}}{2}\).

Crazy!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources