Turn the grid of numbers forty-five degrees to make a triangle of numbers:

The grid presented this way made famous by French mathematician Blaise Pascal (1623-1662) for his work in probability theory.

Each row of this triangle is a diagonal of the original grid and each entry in the triangle counts paths. (If you like, we can make this explicit by counting downward moving paths in a honeycomb.)

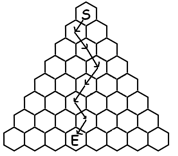
As before,

EACH INTERIOR ENTRY OF PASCAL’S TRIANGLE IS THE SUM OF THE

TWO ENTRIES ABOVE IT

We also have formulas for the individual entries of Pascal’s triangle. The entry that was in the \(a\)th row and \(b\)th column in the original grid (starting our counts with zero-th rows and zero-th columns) is now in the \((a+b)\)th row of Pascal’s triangle, \(a\) places in from the left and \(b\) places in from the right along that row.

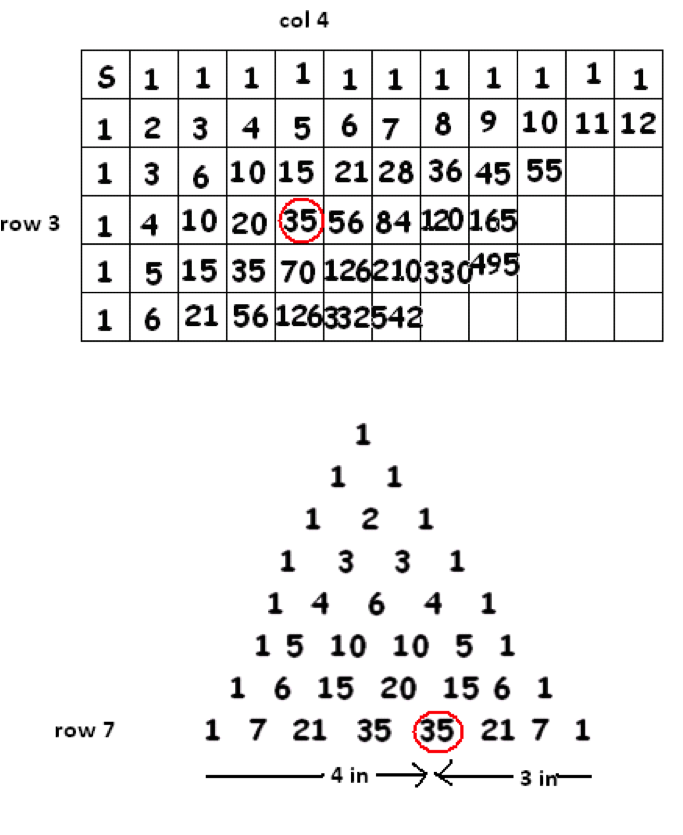
Regard the top row (consisting of the single 1) as the zero-th row of the triangle. The formula for the entry on row \(n\), \(a\) places in from the left and \(b\) places in from the right is:

\(\dfrac{n}{a!b!}\).

(And \(n\) does equal \(a+b\).)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources