[This material appears in Section 2 of the full course on Quadratics.]

 

Our goal now is to recognize complicated expressions as simple level 1 quadratics in disguise. This is level 2.

 

EXAMPLE: Solve \(x^{2}+4x+4=25\).

Answer: Let’s draw a square whose area, hopefully, is \(x^{2}+4x+4\).

 

There is an \(x^{2}\)  piece that must come from \(x \times x\).

Because we want the figure to be a perfectly symmetrical square (squares are good for level 1) the “\(4x\) ” must come from two symmetrical pieces: \(2x\) and \(2x\).

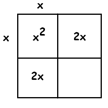
This means we must have the numbers \(2\) and \(2\) on the sides of the square, and this is consistent with the final portion being \(4\).

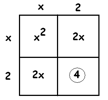
Thus we see that \(x^{2}+4x+4\) is really \((x+2)^{2}\) in disguise, and we just need to solve

\((x+2)^{2} = 25\).

And this is straightforward.

\(x+2=5\)    or    \(x+2=-5\)

\(x=3\)    or    \(x=-7\).

 

EXAMPLE 2: Solve \(x^{2}-10x+25=169\).

Answer: Let’s draw the square for \(x^{2}-10x+25\).

There is an \(x^{2}\) piece that must come from \(x \times x\) . And we need two (symmetrical) pieces that add to \(10x\).

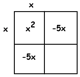
This means the need the numbers \(-5\) and \(-5\), which is consistent with the final portion of the square being \(25\).

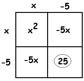
\(x^{2}-10x+25=169\)

\((x-5)^{2}=169\)

\(x-5=13\)    or    \(x-5=-13\)

\(x=18\)   or   \(x=-8\)

 

EXAMPLE: Solve \(x^{2}-20x+100=7\).

Answer: We have:

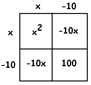
\(x^{2}-20x+100=7\)

\((x-10)^{2}=7\)

\(x-10=\sqrt 7\)    or   \(x-10=-\sqrt 7\)

\(x=\sqrt 7 + 10\)    or   \( x= -\sqrt 7 +10\)

 

EXAMPLE: Solve \(x^{2} +2 \sqrt 5 x + 5 = 4\).

Answer: Don’t be perturbed by the numbers. Just follow things through as before.

Do you see we have this square?

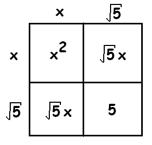
\(x^{2} +2 \sqrt 5 x + 5 = 4\)

\((x+\sqrt5)^{2} = 4\)

\(x+\sqrt5 = 2\)    or    \(x+\sqrt5 = -2\)

\(x=2-\sqrt5\)    or    \(x=-2-\sqrt5\)

 

EXERCISE 1: Solve:

a) \(x^{2}+40x+400=100\)

b) \(p^{2}-6p+9=9\)

c) \(x^{2}-4x+4=1\)

d) \(3x^{2}-18x+27=12\)

e) \(x^{2}-2\sqrt2 x+2=19\)

EXERCISE 2: Solve \(x^{2}+2Bx+B^{2}=D^{2}\)  in terms of \(B\) and \(D\).

 

 

LEVEL 3 QUADRATICS

EXAMPLE: Solve \(x^{2}+8x+15=80\).

Answer: Let’s apply the technique of level 2 and draw the box.

The \(x^{2}\) piece must come from \( x \times x\). And because we want the symmetry of a square, \(8x\) must come for two pieces \(4x\) each.

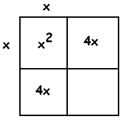
This means we must have the numbers \(4\) and \(4\) on the sides of the square, giving us \(16\) for the remaining piece of the squares, which is inconsistent with the number \(15\) in the problem.

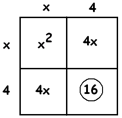
It seems the box method is of no help. We have two options:

1. Weep and give up.
2. Just make it work!

Let’s follow option 2 making use of a good piece of general advice:

If there is something in life you don’t like, change it! (And deal with any consequences.) 

In this problem we would like the number \(15\) in \(x^{2}+8x+15\) to actually be a \(16\). So let’s just add \(1\) and make it \(16\)!

Of course, to keep the equation balanced, if we add \(1\) to one side of an equation we need to add \(1\) to the other side as well.

\(x^{2}+8x+15+1=80+1\).

That is, we have

\(x^{2}+8x+16=81\).

And the box tells us that this is

\((x+4)^{2}=81\).

All now falls into place:

\(x+4=9\)    or    \(x+4=-9\)

\(x=5\)     or    \(x=-13\)

 

EXAMPLE: Solve \(x^{2} -6x+11=27\).

Answer: The box tells us that the \(x^{2}\) and the \(-6x\) pieces want the number \(9\) to accompanying them, not \(11\).

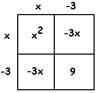
Let’s make that happen. Subtract \(2\) from both sides.

\(x^{2}-6x+9=25\)

\((x-3)^{2}=25\)

\(x-3=5\)    or    \(x-3=-5\)

\(x=8\)    or    \(x=-2\)

 

EXAMPLE: Solve \(x^{2}-10x+3=0\).

Answer: The box tells us that the \(x^{2}\) and the \(-10x\) pieces want the number \(25\) to accompanying them, not \(3\).

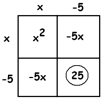
So let’s add \(22\) to both sides to make that happen!

\(x^{2}-10x+3=0\)

\(x^{2}-10x+25=22\)

\((x-5)^{2}=22\)

\(x-5=\sqrt22\)    or    \(x-5=-\sqrt22\)

\(x=5+\sqrt 22 \)    or    \( x=5- \sqrt 22 \)

 

EXAMPLE: Solve \(x^{2}-6x=55\).

Answer: To obtain a perfect square add \(9\) to both sides.

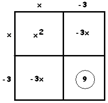
\(x^{2}-6x+9=64\)

\((x-3)^{2}=64\)

\(x-3=8\)    or    \(x-3=-8\)

\(x=11\)    or    \(x=-5\) .

 

EXAMPLE: Solve \(w^{2}+90=22w-31\).

Answer: Let’s bring all the terms containing the variable to the left side.

\(w^{2}-22w+90=-31\).

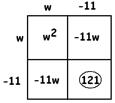
The box tells us to add \(31\) to each side.

\(w^{2}-22w+121=0\)

\((w-11)^2=0\)

\(w-11=0\)

\(w=11\)

 

EXERCISE 3: Solve:

a) \(x^{2}+12x-5=40\)

b) \(z^{2}+2z+3=11\)

c) \(x^{2}-40x+300=69\)

d) \(2f^{2}-16f+30=48\)

e) \(x^{2}+100x+2=3\)

EXERCISE 4: Solve \(x^{2}+3x+1=5\). Don’t be afraid of fractions. You can handle them!

 

LEVEL 4 QUADRATICS 

 

EXAMPLE: Solve \(x^{2}+3x+1=5\).

Answer: Solving this problem does indeed require the use of fractions:

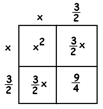
Adding \( 1\frac{1}{4}\) to both sides gives

\(x^{2}+3x+ \frac{9} {4} = 5 + 1 \frac {1} {4}\)

\((x+\frac {3} {2})^{2} = 6 \frac {1} {4}\)

\((x+ \frac {3} {2})^{2} = \frac {25} {4}\)

\( x + \frac {3} {2} = \frac {5} {2} \)    or    \(x + \frac {3} {2} = – \frac {5} {2}\)

\( x = 1\)    or    \(x=-4\)

However, most people would prefer to not work with fractions.

 

The problem here is that the middle term, the \(3x\), has an odd number for a coefficient. So … If we don’t like that, let’s change it!

 

Perhaps the easiest way to create an even number in the middle is to multiply everything through by 2, so \(x^{2}+3x+1=5\) becomes

\(2x^{2} + 6x + 2=10\).

Comment: Some students might say it would be simpler to add \(x\) to both sides to then obtain \(x^{2} + 4x + 1 = 5+x\). But then we have \(x\)’s on both sides of the equation, which is annoying.

 

Okay … Let’s try the box method on \(2x^{2} + 6x + 2=10\).

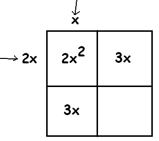
But we have a problem now with the very first piece of the equation: We need two symmetrical terms that multiply together to make \(2x^{2}\). Most students would suggest \(2x\) and \(x\), but this right away ruins the square method we’ve been following in levels 1, 2, and 3. Hmm.

 

It takes an epiphany, but eventually one thinks …

Instead of multiplying through by 2, multiply through by 4.

This again makes the middle term even AND solves the problem with the first term. Let’s see why.

 

Start with: \(x^{2}+3x+1=5\).

Multiply through by 4:

\(4x^{2}+12x+4=20\).

Now apply the box method.

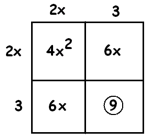
We see that \(4x^{2}\) comes from \(2x\) multiplied with \(2x\), preserving the symmetry.

Notice that the middle term \(12x\) splits into two equal pieces, \(6x\) plus \(6x\), as planned, which means we need the numbers \(3\) and \(3\) on the sides ( \(2x\) times THREE gives \(6x\)).

We also see that the number we need from the box is \(9\). Adding \(5\) to both sides of the equation \(4x^{2}+12+9=20\) yields

\(4x^{2}+12x+9=25\).

The box shows that  \(4x^{2}+12x+9\) is really \((2x+3)^{2}\), so we have a level 1 problem:

\((2x+3)^{2}=25\)

\(2x+3=5\)    or    \(2x+3=-5\)

\(2x=2\)    or    \(2x=-8\)

\(x=1\)    or    \(x=-4\)

IF THE MIDDLE TERM IS ODD, MULTIPLYING THROUGH BY \(4\) IS A CLEVER IDEA!

 

EXAMPLE: Solve \(x^{2}-5x+6=2\).

Answer: Let’s multiply through by \(4\).

\(4x^{2}-20x+24=8\)

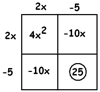
Adding \(1\) to both sides gives:

\(4x^{2}-20x+25=9\)

\((2x-5)^2=9\)

\(2x-5=3\)    or    \(2x-5=-3\)

\(2x=8\)    or    \(2x=2\)

\(x=4\)    or    \(x=1\)

 

EXAMPLE: Solve \(x^{2}+x=\frac {3} {4}\).

Answer: Let’s multiply through by \(4\):

\(4x^{2}+4x=3\)

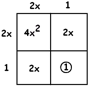
Adding \(1\) to both sides gives:

\(4x^{2}+4x+1=4\)

\((2x+1)^2=4\)

\(2x+1=2\)    or    \(2x+1=-2\)

\(2x=1\)    or    \(2x=-3\)

\(x=\frac {1} {2} \)  or  \(x=-\frac {3} {2}\).

 

EXAMPLE: Solve \(p^{2}+7p-2=5\).

Answer: Let’s multiply through by \(4\).

\(4p^{2}+28p-8=20\)

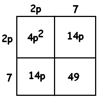
Adding \(57\) to both sides gives:

\(4p^{2}+28p+49=77\)

\((2p+7)^2=77\)

\(2p+7=\sqrt 77\)    or    \(2p+7=-\sqrt77\)

\(2p=\sqrt77 – 7\)    or    \(2p=-\sqrt77 – 7\)

\(p=\frac {\sqrt 77 – 7} {2} \)    or    \(p=\frac {-\sqrt 77 – 7} {2} \)

 

EXERCISE 5: Solve:

a) \(x^{2}+11x-5=7\)

b) \(z^{2}-3z+1=-1\)

c) \(x^{2}-x-1=2 \frac {3} {4}\)

d) \(x^{2} +5x+12=70\)

e) \(x^{2}+3=9\)

EXERCISE 6: OPTIONAL CHALLENGE

At the beginning of this level we first tried solving \(x^{2}+3x+1=5\) by multiplying through by \(2\) to obtain an even middle coefficient.

\(2x^{2}+6x+2=10\).

The trouble with this is that \(2x^{2}\), at first glance, doesn’t seem to be the product of two symmetrical terms.

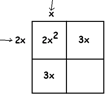
However, if we are willing to work with square roots, it is!

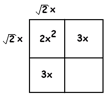
The side term must be a number which multiplies by \(\sqrt2  x\) to give \(3x\).  That would be \( \frac {3} {\sqrt2}\).

The box method is so robust that it will work no matter how or when you choose to try it. Continue the box method to show that our equation \(2x^{2}+6x+2=10\) can be rewritten \( (\sqrt 2 x+\frac {3} {\sqrt 2})^{2}= \frac {25} {2}\), and that this, by level 2, again has solutions \(x=1\) and \(x=-4\).

OKAY .. Now we are ready for the full power of solving quadratics!

Resources