Let’s have some fun with garden paths.

Imagine a garden path with infinitely many forks that split into three parts as shown. Those that turn left at a fork go to house A, those that turn right to house B, and those who go straight continue to the next fork.

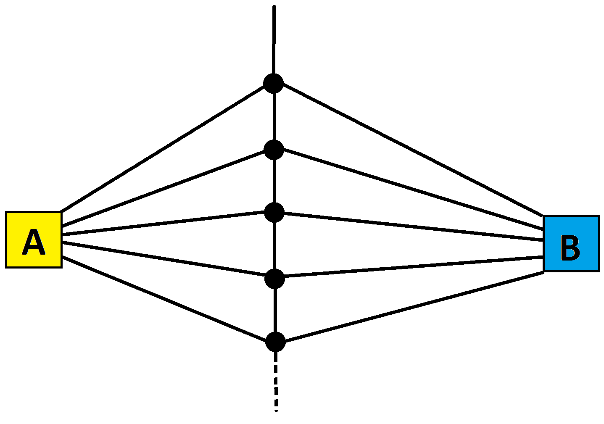
This leads to the area picture:

The probability of ending up in house A is:

\(\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{81}+ \ldots\),

as are the chances of ending up in house B.

But do you see that half the square is devoted to house A and half to house B? It follows then that we must have:

\(\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{81}+ \ldots=\dfrac{1}{2}\).

CHALLENGE: Use garden paths to establish that

\(\dfrac{1}{N}+\dfrac{1}{N^{2}}+\dfrac{1}{N^{3}}+ \ldots = \dfrac{1}{N-1}\)

for any positive integer \(N > 1\).

Can you prove the general geometric series formula \(x+x^{2}+x^{3}+\ldots = \dfrac{x}{1-x}\) for \(0<x<1\) using garden paths?

EXTRA: See Lesson 4.7 as we push this example further and show how it opens the gateway to a host of infinite probability processes!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources