SETTING THE SCENE

The story of quadratrics is really the story utilizing area-thinking in mathematics and coupling it with the power of symmetry. And by taking the time to understand the strength of these two key players in the story, one not only develops a profound understanding of the curriculum topic, but also develops the deep joy and the profound agency that comes from thinking like a mathematician.

It may seem that this brief opening lesson is a diversion from matters at hand, but it is not. The ideas presented here provide the core mind-set of being a mathematician.

We begin with the story of area.

 

RESOURCES:

A PDF of these notes appears here: QUADRATICS PD Essay 1.1. (Many people find it easier to read the PDF file rather than this web presentation of the same notes.)

See Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.

 

 

AREA INFORMS BOTH ARITHMETIC AND ALGEBRA

Consider the arithmetic problem:  Compute \(37 \times 23\).

 

To me, this is really a geometry problem: we are being asked to compute the area of a 37-by-23 rectangle.

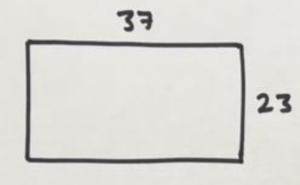
But the numbers are awkward! Can we make matters easier on ourselves in some way?

 

Principle: Mathematicians will always pause and think hard to avoid hard work!

 

It seems natural to break each of the numbers 37 and 23 into friendlier numbers, say 30 and 7, and 20 and 3, and thus divide the rectangle into four pieces whose areas are simple to compute. The area of the rectangle—and thus the answer to \(37 \times 23\)—is \(600+140+90+21=851\).

 

Practice 1: Use the area model to compute \(3721\times223\). (Into how many pieces might you divide your rectangle?)  

Practice 2: Use the traditional long multiplication algorithm to compute \(845 \times 387\). And use it again to compute \(387\times 845\), but as you do so this second time ask yourself: Is it obvious the algorithm will give the same final answer?

(Answers to all the practice problems appear at the end of this page.)

 

Area-thinking informs us of the general behavior of numbers. For example, rotating a 37-by-23 rectangle ninety-degrees gives a 23-by-37 rectangle. The area of the rectangle does not change in this process, so it must be the case that gives the same answer .

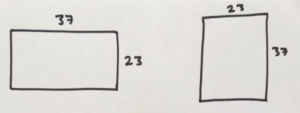
In general, rotating a picture of a rectangle 90-degrees shows that

\(a \times b = b \times a\)

for all numbers that can be the side-lengths of rectangles.

In the early grades, we know only of the positive counting numbers, and the area model shows that \(a\times b= b \times a\) for all positive counting numbers. But as our schooling progresses, we learn of other types of numbers. We can imagine rectangles with fractional side lengths, and so we come to believe that \(a \times b = b \times a\)  holds true for all fractions as well.

 

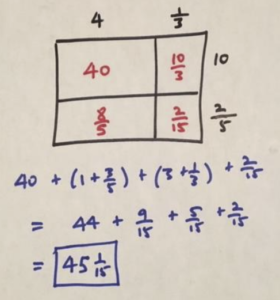
Practice 3: Use the area model to compute \(4\frac{1}{3}\times 10\frac{2}{5}\) .

 

And we can imagine rectangles with irrational number side-lengths and so we believe that \(a\times b= b \times a\) holds for irrational numbers as well.

And this belief, by this point, feels so natural and so right that we believe, surely, that \(a\times b= b \times a\) should hold for ALL numbers, even ones that extend beyond geometry, namely, negative numbers.

 

Technically, one cannot have rectangles with negative side-lengths or with negative areas. But we like to believe that if we were to draw pictures of such rectangles they will still speak truth about arithmetic, that \(a\times b= b \times a\) holds too for negative numbers, for instance.

 

Upshot: We like to believe that rectangle diagrams speak truth about arithmetic for all types of numbers, even if the numbers are technically not valid in geometry.

 

This belief now answers and age-old-question: Why, in mathematics, is negative times negative positive?

 

Just to be clear on the basics …

We all agree that positive times positive is positive. For example, \(3 \times 2\), interpreted as “three groups of two,” has answer \(2+2+2=6\), positive six.

And most people are comfortable saying that positive times negative is negative. For instance, \(3 \times (-2)\) is “three groups of negative two” and so has value \(-2+-2+-2=-6\), negative six.

Matters become trickier with negative times positive. For instance, reading \((-3)\times 2\) as “negative three groups of two” makes no sense! But armed with our belief that \(a\times b= b \times a\) holds true for ALL types of numbers, we can argue then that \((-3)\times 2\) equals \(2\times(-3)\), and so is “two groups of negative three” and thus has value \(-3+-3=-6\), negative six.

But trouble comes with negative times negative. What is \((-3)\times (-2)\)? We’ve all been trained to say “positive six.” But why? “Negative three groups of negative two” makes no sense. Nor does “negative two groups of negative three.” Switching the order of the terms does not help.

 

Why negative times negative is positive

Let’s compute \(17 \times 18\) four different ways!

We can compute it be breaking up the numbers \(17\) and \(18\) in the expected ways to see the answer \(306\).

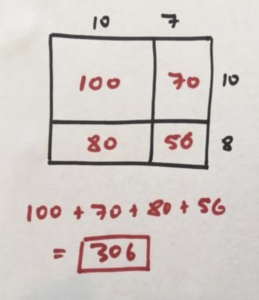
Or we try something unexpected with the number \(17\) and think of it as \(20+(-3)\). Since we know negative \(\times\) positive and positive \(\times\) negative are both negative, we can complete the diagram and see the answer \(306\) appear again. (The diagram speaks arithmetic truth!)

We can see the answer \(306\) yet again in thinking of \(18\) as \(20+(-2)\).

But let’s now write both \(17\) and \(18\) in their unexpected ways. We see the diagram needs the answer to \((-3)\times (-2)\). But we know, from three computations now, that \(17\times 18=306\).

 

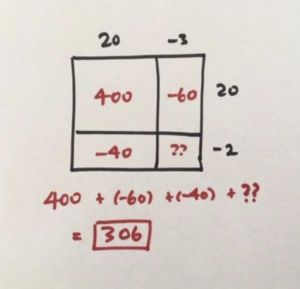
The mathematics shows that we have no choice but to set \((-3)\times (-2)=6\), positive six!

 

Upshot: Our belief that all numbers obey the same rules of arithmetic inspired by geometry forces us to conclude that negative times negative is positive.

 

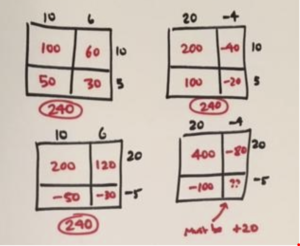
Practice 4: Compute \(16 \times 15\) four different ways to conclude that \((-4)\times (-5)\) is positive \(20\) .

 

Since the area model speaks truth for all numbers we can use it too in algebra. For instance, the area model shows that \(\left(2x+1\right)\times\left(3x+7\right)\) equals \(6x^2+17x+7\). And this is true no matter the value of \(x\): positive or negative!

 

 

Practice 5:  a) Use the area model to compute \(\left(2x^2+x+1\right)\left(3x+2\right)\). 

b) Use your answer to quickly see the value of \(211 \times 32\).

c) Put \(x=-10\) into your answer from a). What multiplication problem is this the answer to?

   

THE POWER OF SYMMETRY

Here’s a rectangle. I tell you its area is 36 square units. What can you tell me about the rectangle?

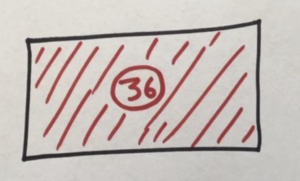
Answer: Nothing! It might be a 4-by-9 rectangle, or a 2-by-18 rectangle, or a 4½-by-8. You don’t know. You only know that it’s area is 36 square units.

But suppose I now add one more piece of information about this rectangle, that it is symmetrical. Now you know everything about that rectangle. It must be a 6-by-6 square!

This illustrates the power of symmetry in mathematics. Often the introduction of symmetry in a scenario collapses unknown information into crystalline precise information.

 

Principle: Mathematicians recognize the power of symmetry. Symmetry is a mathematician’s friend!

 

To illustrate the power of symmetry, let’s end off with a classic textbook problem in the study of quadratrics—even though we have not yet introduced what a quadratic is! We can solve the problem just with the joy of symmetry.

 

Example: A farmer has 40 meters of fencing and wants to use it all to make a rectangular pen. What should the dimensions of the rectangle be to obtain a pen of maximal possible area?

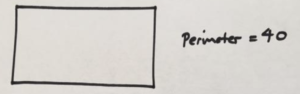
Answer: Let’s consider the symmetrical situation first: a pen that is a square. Since the perimeter of the pen is 40 meters, this would be a 10-by-10 square.

But we have no reason to believe that a square pen is the one of maximal area. In general, a pen will have one side longer than 10 meters and the other shorter than 10 meters. Let’s measure the dimensions of a general pen by recording the degree to which it deviates from being a symmetrical square pen. Let’s consider a \(10+x\)-by-\(10-x\) pen for some number \(x\).

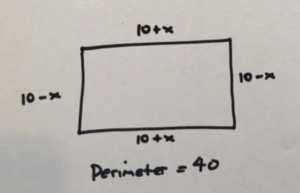
The area this pen is

\(\left(10+x\right)\left(10-x\right)=100+10x-10x-x^2=100-x^2\).

And what value of \(x\) gives a maximal value for the area formula \(100-x^2\)? Clearly \(x=0\) gives the maximal area. So the pen that does not deviate at all from being a square pen is the one of maximal area! The farmer should build a 10-by-10 pen. 

 

Practice 6: (CHALLENGE) A farmer has 40 meters of fencing and wants to use it all to make a rectangular pen. But she has huge mirrored wall in her field and wants to use the mirror as one side of her rectangular pen.

 

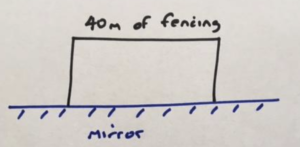
What should the dimensions of the rectangle be in order to obtain a pen of maximal area?

 

Principle: Mathematicians will attempt to push the results of a previously solved problem to help with a new problem.

 

 

 

SOLUTIONS

 

Practice 1: Use the area model to compute \(3721\times 223\). (Into how many pieces might you divide your rectangle?) 

 

Answer: One might divide a rectangle into twelve pieces by thinking of \(3721\) as 3000 + 700 + 20 + 1 and \(223\) as 200 + 20 + 3. The areas of the individual pieces then add to \(829783\).

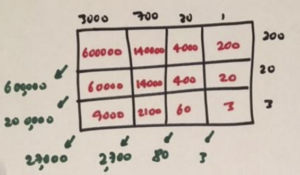
Of course, one need not divide the rectangle this way. One could think of \(3721\) as 2000 + 1500 + 10 + 10 + 1 and \(223\) as 100+100+10+10+1+1+1, for instance.

All ways of subdividing the rectangle should, of course, yield the same final answer of 829783.

 

 

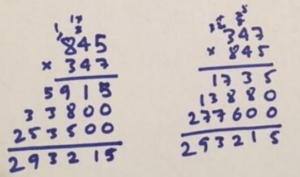
Practice 2: Use the traditional long multiplication algorithm to compute \(845 \times 387\). And use it again to compute \(387\times 845\), but as you do so this second time ask yourself: Is it obvious the algorithm will give the same final answer?

 

Answer: It is not at all obvious to me why at face value the traditional long multiplication algorithm naturally gives the same answers whether you compute \(a\times b\) or \(b \times a\). What you write on the page looks different. It is actually somewhat surprising that the final lines after each summation are the same.

 

Practice 3: Use the area model to compute \(4\frac{1}{3}\times 10\frac{2}{5}\).

 

Answer:

 

Practice 4: Compute \(16\times 15\) four different ways to conclude that \((-4)\times (-5)\) is positive \(20\).

Answer:

 

 

Practice 5:  a) Use the area model to compute \(\left(2x^2+x+1\right)\left(3x+2\right)\). 

b) Use your answer to quickly see the value of \(211 \times 32\).

c) Put \(x=-10\) into your answer from a). What multiplication problem is this the answer to?

 

Answer:

a) \(\left(2x^2+x+1\right)\left(3x+2\right) = 6x^3+7x^2+5x+2\)

 

b) Put \(x=10\) to see that this reads: \(\left(200+10+1\right)\left(30+2\right)\) equals \(6000+700+50+2=6752.\)

c) We have \(\left(200-10+1\right)\left(-30+2\right)\), that is, \(191 \times (-28)\), equals \(-6000+700-50+2\), which is \(-5348\).

 

Practice 6: (CHALLENGE) A farmer has 40 meters of fencing and wants to use it all to make a rectangular pen. But she has huge mirrored wall in her field and wants to use the mirror as one side of her rectangular pen.

What should the dimensions of the rectangle be in order to obtain a pen of maximal area?

 

Answer:  This problem is not-symmetrical as the pen has two full vertical sides and only one horizontal side. The problem we discussed in the essay just before this was symmetrical with two sides of each type.

But if one looks into the mirrored wall, it will look as though we have a rectangular pen, double the area and double the perimeter (80 meters), with FOUR sides of fencing.

We know the answer to the symmetrical problem is a symmetrical square, so the mirrored reflection must be a 20 meter-by-20 meter square pen to get maximal area. But the actual pen without the reflection is half of this, a 10 meter-by-20 meter pen!

She should build a 10-by-20 pen.

SNEAKY!

Resources