Here is a video from Goldfish & Robin and friends “Where Young Minds Collide” demonstrating the weird 2 <– 3 machine. 

 

Let’s get weird!

 

What do you think of a \(1 \leftarrow 1\) machine?

What happens if you put in a single dot? Is a \(1 \leftarrow 1\) machine interesting? Helpful?

 

What do you think of a \(2 \leftarrow 1\) machine?

What happens if you put in a single dot?

What do you think of the utility of a \(2 \leftarrow 1\) machine?

 

After pondering these machines for a moment you might agree there is not much one can say about them. Both fire “off to infinity” with the placement of a single dot and there is little control to be had over the situation.

 

How about this then?

 

What do you think of a \(2 \leftarrow 3\)machine?

This machine replaces three dots in one box with two dots one place to their left.

 

Ah! Now we’re on to something. This machine seems to do interesting things.

 

For example, placing ten dots into the machine

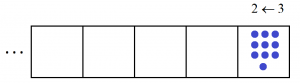
first yields three explosions,

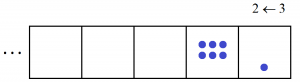
then another two,

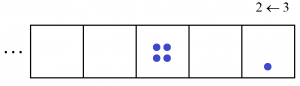
followed by one more.

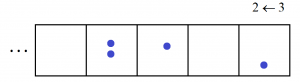
We see the code \(2101\) appear for the number ten in this \(2 \leftarrow 3\) machine.

 

In fact, here are the \(2 \leftarrow 3\) codes for the first fifteen numbers. (Check these!)

 

Question: Does it make sense that only the digits \(0\), \(1\), and \(2\) appear in these codes?

Question: Does it make sense that the final digits of these codes cycle \(1,2,0,1,2,0,1,2,0,\ldots\)?

 

One can do arithmetic in this weird system! For example, ordinary arithmetic says that \(6+7=13\) and the codes in this machine say the same thing too!

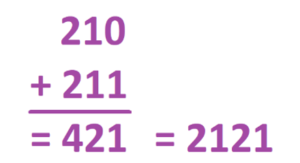
But the real question is:

What are these codes? What are we doing representing numbers this way? Are these codes for place-value in some base?

 

Of course, the title of this section gives the answer away, but let’s reason our way through the mathematics of this machine.

 

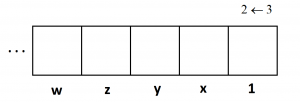
Dots in the rightmost box, as always, are each worth \(1\). Let’s call the values of dots in the remaining boxes \(x\), \(y\), \(z\), \(w\), ….

Now three dots in the \(1\)s place are equivalent to two dots in the \(x\) place.

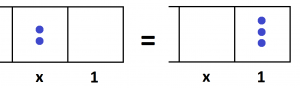
This tells us that \(2x=3\cdot\), giving the value of \(x=\dfrac{3}{2}\), one-and-a-half.

In the same was we see that \(2y=3 \cdot \dfrac{3}{2}\).

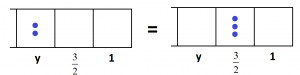
This gives \(y=\dfrac{3}{2}\cdot \dfrac{3}{2}=\left(\dfrac{3}{2}\right)^2\), which is \(\dfrac{9}{4}\).

 

And in the same way,

\(2z=3\left(\dfrac{3}{2}\right)^2\) giving  \(z=\left(\dfrac{3}{2}\right)^3\), which is \(\dfrac{27}{8}\),

\(2w=3\left(\dfrac{3}{2}\right)^3\) giving \(w=\left(\dfrac{3}{2}\right)^4\), which is \(\dfrac{81}{16}\),

and so on.  We are indeed working in something that looks like base one-and-a-half! (It was discovered

 

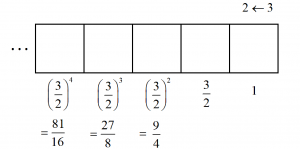
Comment: This version of base one-and-a-half was discovered by mathematician Jim Propp. It is a little unusual as it uses the digit “2,” which is larger than than base number. Other versions of base-one-and-a-half  are called beta expansions and non-integer representations. In these notes, when I refer with “base one-and-a-half”  I’ll follow Jim Propp’s version: the representations of integers as sums of powers of one-and-a-half using the coefficients 0, 1, and 2 a la the \(2 \leftarrow 3\) machine.

 

I personally find this version of base one-and-a-half intuitively alarming! We are saying that each integer can be represented as a combination of the fractions \(1\), \(\dfrac{3}{2}\), \(\dfrac{9}{4}\), \(\dfrac{27}{8}\), \(\dfrac{81}{16}\), and so on. These are ghastly fractions!

 

For example, we saw that the number ten has the code \(2101\).

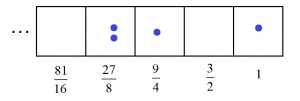
Is it true that this combination of fractions, \(2 \times \dfrac{27}{8}+1\times \dfrac{9}{4}+0\times \dfrac{3}{2}+1\times 1\), turns out to be the perfect whole number ten?  Yes! And to that, I say: whoa!

 

There are plenty of questions to be asked about numbers in this \(2 \leftarrow 3\) machine version of base one-and-a-half, and many represent unsolved research issues of today! For reference, here are the codes to the first forty numbers in a \(2 \leftarrow 3\) machine (along with zero at the beginning).

 

QUESTION: PATTERNS?

Are there any interesting patterns to these \(2 \leftarrow 3\) machine code representations?

 

Why must all the representations (after the first) begin with the digit 2?

Do all the representations six and beyond begin with 21?

If you go along the list far enough do the first three digits of the numbers become “stable”?

 

What can you say about final digits? Last two final digits?

Is there a code that ends with 2200?

 

Comment: Dr. Jim Propp of UMass Lowell, who opened my eyes to the \(2 \leftarrow 3\) machine suggests these more robust questions.

 

What sequences can appear at the beginning of infinitely many \(2 \leftarrow 3\)  machine codes?

What sequences can appear at the end of infinitely many \(2 \leftarrow 3\) machine codes?

 

I happen to know the answer to the latter question: any finite seqeuence of \(0\)s, \(1\)s, and \(2\)s can be the trailing end of a \(2\leftarrow 3\) machine code. Here’s a sequence of thoughts you can follow to see why.

1. Show that \(N=3^k\) has a \(2 \leftarrow 3\) machine code that ends with \(k\) zeros and has either a \(1\) or a \(2\) just to their left. (Which \(k\) give a \(1\) and which \(k\) give a \(2\)?)

2. Explain why \(N\), \(2N\), and \(3N\) each have codes that end with \(k\) zeros and have, in some order, either the digit \(1\), \(2\), and \(0\) just to their left.

3. Suppose I wish to find a number whose machine code ends 10221. Can you see how to construct \(N=3^0+3^1+2\cdot 3^2+3^3 +2 \cdot 3^4\) as one such number?

 

QUESTION:  DIVISIBILITY RULES

Divisibility by 3, and other powers of three.

Look at the list of the first forty \(2\leftarrow 3\) codes of numbers. As soon as one realizes why the final digit of these codes cycle through the value 0, 1 and 2, the following divisibility rule for 3 appears.

 

     A number written in \(2\leftarrow 3\)  code is divisible by three precisely when its final digit is zero.

 

Challenge: Find, and explain, a divisibility rule for 9. Find ones for 27 ,81, and 243 too.

 

Divisibility by 5

Can you explain this divisibility rule for five?

 

A number is divisible by 5 only if the alternating sum of its \(2\leftarrow 3\)  machine code digits is a multiple of five.

 

For example, twenty has code \(21202\) and \(2-1+2-0+2\) is a multiple of five. And forty has code \(2101121\) and \(2-1+0-1+1-2+1=0\) is a multiple of five. And eleven has code \(2102\) and \(2-1+0-2=-1\) is not a multiple of five.

 

Comment: See Experience 12 for “Puzzles Explained by Exploding Dots.” This is one of the puzzles discussed.

 

Divisibility by 2

What is a divisibility rule for the number two for numbers written in \(2\leftarrow 3\)  code? What common feature does every second code have?

I personally do not know a swift way to tell whether or not a number is even just by looking at its \(2 \leftarrow 3\) machine code. If you find one, let me know!

 

By the way ….

 

Delete the final digit of the \(2 \leftarrow 3\)  machine code of an even number and what results is the machine code of another even number.

 

For instance, forty has code 2101121. Delete the final digit and you get 210112, which is the code for the even number twenty-six. Delete its final digit and you get 21011 (eighteen), then 2101 (ten), then 210 (six), then 21 (four), then 2 (two).

 

Why does this property hold? Why does deleting the final digit give you two-thirds of the original number rounded down to an integer?

 

 

QUESTION: UNIQUENESS OF CODES?

The \(2 \leftarrow 3\) machine shows that each and every whole number can be written as a sum of powers of \(\dfrac{3}{2}\) using the coefficients \(0\), \(1\), and \(2\).

Now show that these representations are unique in the sense that no whole number can be written as a sum of powers of \(\dfrac{3}{2}\) using the coefficients \(0\), \(1\), and \(2\) in more than one way.

 

Hint: if \(a{\left(\dfrac{3}{2}\right)}^{r}+b{\left(\dfrac{3}{2}\right)}^{r-1}+\cdots + c\left(\dfrac{3}{2}\right)+d = e{\left(\dfrac{3}{2}\right)}^{s}+f{\left(\dfrac{3}{2}\right)}^{s-1}+\cdots + g\left(\dfrac{3}{2}\right)+h\), why must \(d=h\)?

 

In the same way, prove that every whole number can be uniquely written as sums of non-negative powers of \(\dfrac{7}{5}\) using the coefficients \(0,1,2,3,4,5,6\). And that every whole number can be uniquely written as sums of non-negative powers of \(\dfrac{10}{7}\) using the coefficients \(0,1,2,3,4,5,6,7,8,9\). And that every whole number can be uniquely written as sums of non-negative powers of \(\dfrac{339}{56}\) using the coefficients \(0,1,\ldots,338\). And so on!]

 

QUESTION:  IS IT AN INTEGER?

Not every collection of \(0\)s, \(1\)s, and \(2\)s will represent a whole number code in the \(2 \leftarrow 3\) machine. For example, looking at the list of the first forty codes we see that \(201\) is skipped. This combination of powers of one-and-a-half thus is not an integer. (It’s the number \(5\frac{1}{2}\).)

 

Here’s a question:

Is \(21022120202120020122011201102202010221020100202212\) the code for a whole number in a \(2 \leftarrow 3\) machine?

Of course, we can just work out the sum of powers this represents and see whether or not the result is a whole number. But that doesn’t seem fun!

Is there some quick and efficient means to look as a sequence of \(0\)s, \(1\)s, and \(2\)s and determine whether or not it corresponds to a code of a whole number? (Of course, how one defines “quick” and “efficient” is up for debate.)

 

QUESTION:  COUNT OF DIGITS

Looks again at the first forty \(2 \leftarrow 3\) codes.

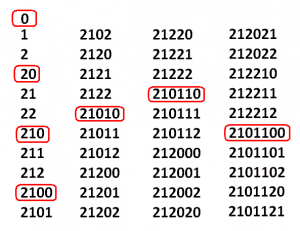
Notice

0 gives the first one-digit code. (Some might prefer to say  here.)

3 gives the first two-digit code.

6 gives the first three-digit code.

9 gives the first four-digit code.

and so on.

This gives the sequence: 3, 6, 9, 15, 24, …. (Let’s skip the questionable start.)

 

Are there any patterns to this sequence?

 

If you are thinking Fibonacci, then, sadly, you will be disappointed with the few numbers of the sequence.

\(36, 54, 81, 123, 186, 279, 420, 630, \ldots\) 

 

A Recursive Formula

Let \(a_{N}\) represent the \(N\)th number in this sequence, regarding \(1\) as the first one-digit answer.  It is known that

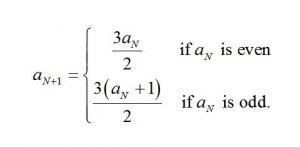
(If \(m\) dots are needed in the rightmost box to get a code \(N\) digits long, how many dots do we need to place into the \(2 \leftarrow 3\) machine to ensure that \(m\) dots appear the second box? This will then give us a code \(N+1\) digits long.)

 

An Explicit Formula?

Is there an explicit formula for \(a_{N}\)? Is it possible to compute \(a_{1000}\) without having to compute \(a_{99}\) and \(a_{98}\) and so on before it?

 

(This question was posed by Dr. Jim Propp.)

 

FURTHER: There is a lot of interest about problems involving the power of two, and three, and of three-halves. See Terry Tao’s 2011 piece , for instance.

Also see “On Base 3/2 and its Sequences” by ben Chen et al (August, 2018) at arXiv:1808.04304 [math.NT] for additional work on the codes of numbers that arise from a  machine.

 

QUESTION:  COUNTING EXPLOSIONS

The following table shows the total number of explosions that occur in the \(2 \leftarrow 3\) machine to obtain the code of each of the first forty numbers.

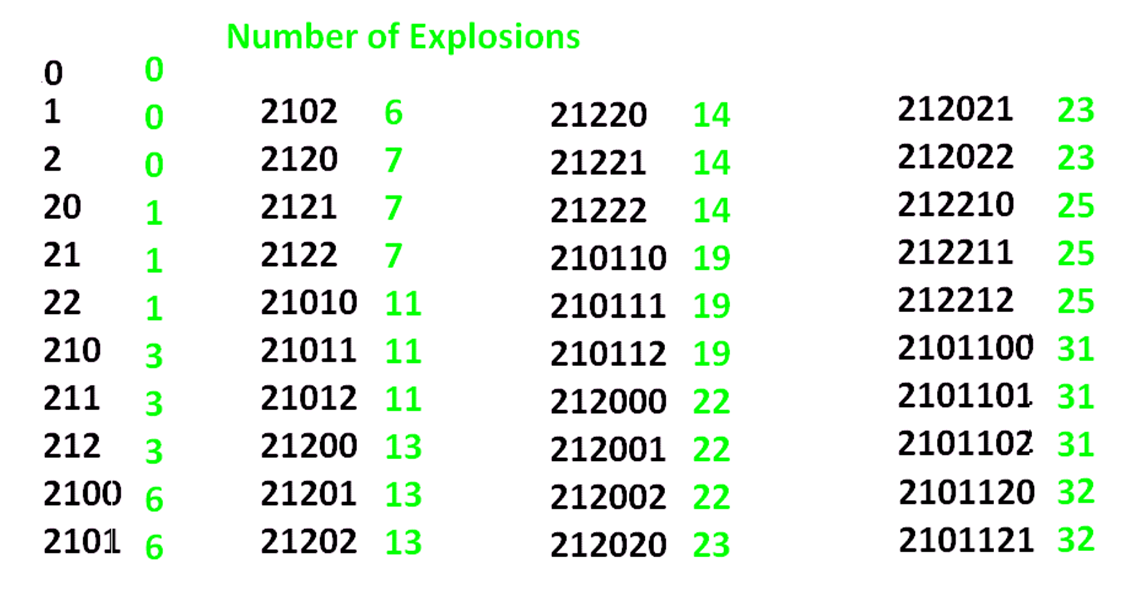
Any patterns?

 

 

QUESTION: DECIMALS

It seems like we should be able to construct “decimals” in a \(2\leftarrow 3\) machine.

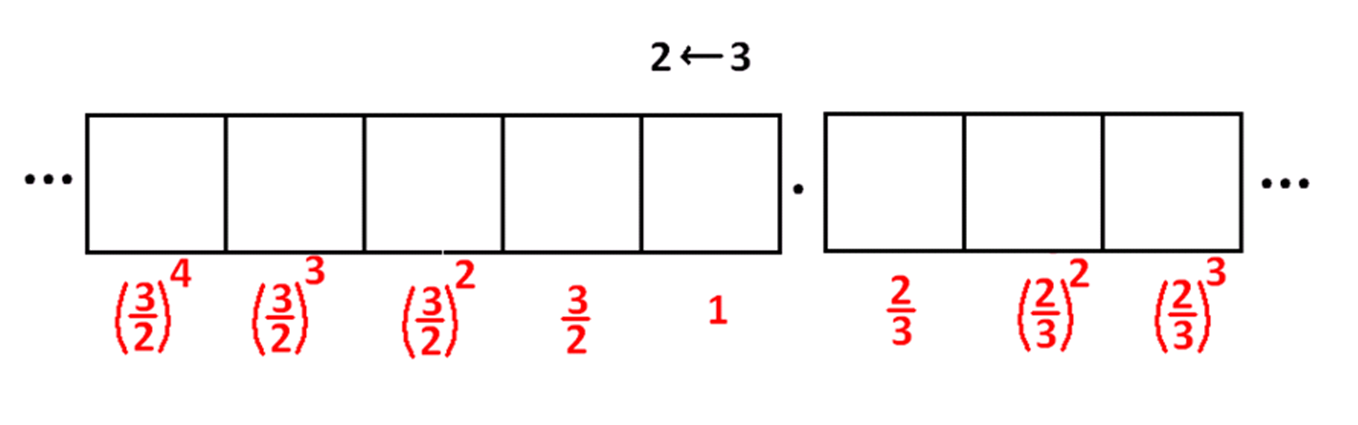
We can certainly evaluate finite decimals. For example:

\(0.1=\dfrac{2}{3}\)

\(0.02=\dfrac{8}{9}\)

\(0.12=\dfrac{28}{27}\)

 

And we can evaluate some infinitely long decimals. For example:

\(0.11111\ldots = {\left(\dfrac{2}{3}\right)}+{\left(\dfrac{2}{3}\right)}^2+{\left(\dfrac{2}{3}\right)}^3+{\left(\dfrac{2}{3}\right)}^4+\cdots = \dfrac{2/3}{1-2/3}=2\)

\(o.12121212\ldots = \dfrac{5}{3}\)

 

Question: Does every repeating “decimal” in this machine correspond to a rational value?

Question: Does every rational value have a repeating decimal expression?

 

This second question is mysterious to me. Can the fraction \(\dfrac{1}{2}\) be represented as a “decimal” in this machine? How does one perform the division computation \(1 \div 2\) in a \(2\leftarrow 3\) machine? If it has a decimal representation, is the representation unique?

 

One can always perform a “greedy algorithm” approach to computing a decimal expansion: simply subtract off the largest power of two-thirds or double two-thirds one stage at a time. For example

\(\dfrac{1}{2}=1 \times \dfrac{4}{9}+ more\)

\(\dfrac{1}{2}-\dfrac{4}{9}=\dfrac{1}{18}=1 \times {\left(\dfrac{2}{3}\right)}^{8}+ more\)

\(\dfrac{1}{2}-{\left(\dfrac{2}{3}\right)}^{2}-{\left(\dfrac{2}{3}\right)}^{8}=1 \times {\left(\dfrac{2}{3}\right)}^{11}+ more\)

etc

 

and this gives

\(\dfrac{1}{2}=0.0100000100100101000000000100000010001000000100100101\ldots\)

 

This matches what WolframAlpha gives if you type in “1/2 on base 1.5”.

Question: Is there a repeating pattern to this representation? If not, does \(\dfrac{1}{2}\) have a different, but repeating, representation?

 

ULTIMATE CHALLENGE: Develop a general theory about which fractions have repeating “decimal” representations in the \(2 \leftarrow 3\) machine.

 

Another Challenge: Using the thinking of Experience 10, it is possible to write the fraction \(\dfrac{1}{2}\) as an infinitely long period expression in a \(2\leftarrow 3\) machine if you are willing to allow infinitely many digits to the left of the decimal point instead of to the right!

 

 

QUESTION: THE HUNT FOR PALINDROMES

The number \(17\) has code \(21021\) in a \(2 \leftarrow 3\) machine, a palindrome: it reads the same way forwards as backwards.

The codes for 1, 2, 5, 8, 35, 170, 278, 422, and 494 are each also palindromic.

Challenge: Are there any more examples? 

 

Dr. Gary Davis writes about this fun and cool numerical exploration on his site here.

Also look at Dr. James Propp’s beautiful Mathematical Enchantments column.

 

Resources