A natural question: What is an angle?

Loosely speaking, an angle is simply “an amount of turning.”

If I were to twirl in place and end up back facing you, we would say I turned through an angle of one full turn. If I did this a second time (in the same direction) we’d say I had turned through an angle of two full turns.

Twirling through an angle of half a turn would land me with my back to you, as would a twirl of one-and-half full turns, and an angle of 99.5 full turns.

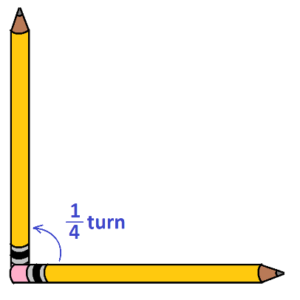
Here’s pencil pointing to the right.

If we turn this pencil a quarter-turn about its end, say in a counter clockwise direction, then its new position relative to its starting position will be as shown.

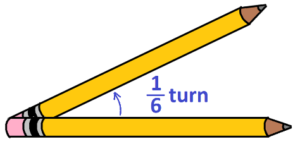
The following picture shows \(\dfrac{1}{6}\) of a turn.

And the following shows a half turn, a full turn, and two full turns of pencils with different starting positions.

Notice that any full count of turns gives the same final effect as applying no turns at all.  (Well, this statement can be questioned. See lesson 1.5 for some curious comments on this!)

Formalities

In school books an angle is depicted with two rays (or just line segments) emanating from a common vertex and this description is often taken as the definition of an angle, stripped of the intuition.

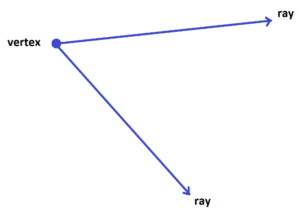
Although “two rays with a common vertex” is a good formalized definition of an angle, it is still useful to keep the idea of an amount of turning explicitly in mind.

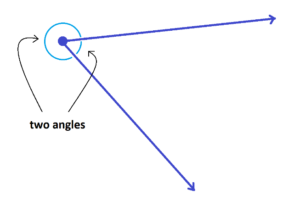
But there is a tiny problem: a diagram of two such rays actually depicts two angles (or more, if you consider multiple full turns plus these angles).  So one must always be careful to clarify exactly which angle is being discussed. If no clarification is offered, then one should assume that the smaller angle, the one representing the least amount of turning, is the one being considered.

Aside: Mathematicians sometimes like to differentiate between positive and negative angles. It has become the convention to regard angles that turn in the counter-clockwise direction as positive and those turning in the clockwise direction as negative.

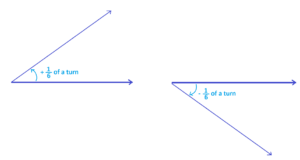
This distinction isn’t made in a typical school course: all angles are considered positive.

Pencil Pushing

Pencils are a very good tool for encoding the physical effect of turning. To get a feel for the angle represented by two line segments with a common vertex drawn on a page simply choose one end of a pencil and place it at the vertex of the diagram, align the whole pencil with one line segment, and then turn the pencil about the chosen end until the pencil aligns with the second line segment. The amount of turning the pencil has undergone is the measure of the amount of turning that angle represents.

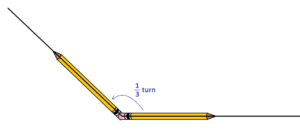
As a hint of the power of this idea, consider this.

Two straight lines that cross create four angles around the intersection point.

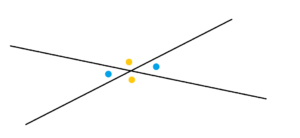
Each pair of angles opposite one another across the intersection point is called a pair of vertical angles–not because the angles are “not horizontal,” but because they are in relation to a vertex, and people choose not to say “vertexical.” (Some people use the term vertically opposite angles.)

So in our diagram the two blue angles are a pair of vertical angles. The pair of yellow angles are also vertical.

One learns in geometry class that vertical angles are congruent, that is, that they represent the same amount of turning. One can experience that with a pencil!

The rightmost blue angle affects a pencil as shown.

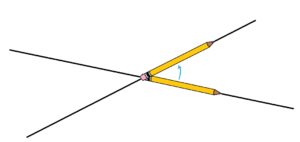
We can see the effect of the leftmost blue angle, with the pencil starting in the same initial position as follows.

1. Place the pencil in the same starting position.

2. Slide the pencil along the line on which it sits so that its tip now sits at the vertex. (This is not changing the direction in which the pencil points. No turning is being applied.)

3. Apply the turning of the leftmost blue angle. This will be tuning about its tip.

4. Slide the pencil along the second line. (This applies no turning to the pencil.)

We see we obtain the same final pencil position, and so both angles applied the same measure of turning to the pencil.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources