Global Math Project Experiences
1.3 Putting Pencil-Pushing to Use
Lesson materials located below the video overview.
People like to say that one full turn corresponds to 360 degrees of turning and use a \(\circ\) superscript to denote a count of degrees.
Question: Why that number? Who chose the number 360 for the count of degrees in a circle? Would you think to choose that number? Let’s talk about this in the next (optional) lesson.
Thus half a turn corresponds to \(\dfrac{1}{2}\cdot 360^{\circ}=180^{\circ}\) of turning, quarter of a turn to \(\dfrac{360^{\circ}}{4}=90^{\circ}\) of turning, two full turns to \(2 \times 360^{\circ}=720^{\circ}\) of turning, and so on.
Question: To how many degrees do the following fractions of turn correspond?
a) \(\dfrac{1}{6}\) of a turn b) \(\dfrac{3}{4}\) of a turn c) one-and-a-half turns
To what fraction of a turn do the following counts of degrees correspond?
d) \(45^{\circ}\) e) \(20^{\circ}\) f) \(1080^{\circ}\) g) \(0.01^{\circ}\)
(See the teacher guide here for solutions.)
People throughout the ages have noticed that there seems to be something special about the three angles inside a triangle—any triangle. It appears that
The three interior angles of a triangle have measures sure to add to half a turn (\(180^{\circ}\)).
And pencil pushing shows this. Try this next activity!
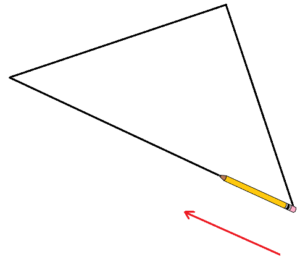
STEP 1: Draw a large triangle on a piece of paper, one large enough to contain a small pencil. (Or draw a large triangle on a chalkboard, or in the sand.)
Place a pencil with one end in the corner of the triangle, aligned with the side of a triangle. Take note of the direction the pencil is initially pointing.
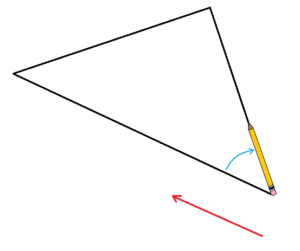
STEP 2: Apply to the pencil the amount of turning of the first angle.
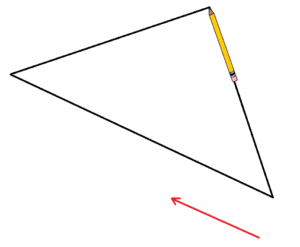
STEP 3: Slide the pencil along the side of the triangle on which it sits. This action applies no turning to the pencil.
STEP 4: Apply to the pencil the amount of turning of the second angle.

STEP 5: Slide the pencil along the side of the triangle on which it sits. This action again applies no turning to the pencil.

STEP 6: Apply to the pencil the amount of turning of the third angle.
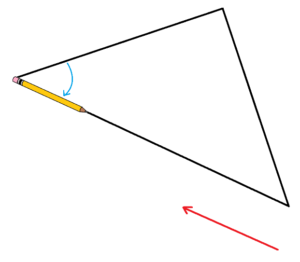
STEP 7: Slide the pencil back to start along the side of the triangle on which is sits.

We see that the pencil is now pointing in the opposite direction to which it started!
The total effect of applying the amount of turning given by the three angles in a triangle is that of a half turn. So indeed,
The three interior angles of a triangle have measures that sum to \(180^{\circ}\).
Can you see in your mind’s eye that for any triangle you happen to draw on the page the same half turn of a pencil would occur? Can you see that the same phenomenon would occur for a pencil moving inside a triangle the size of the solar system? Can you see that it would occur too for a pencil inside a triangle the size of an atom (a sub-atomic sized pencil, of course)? It seems this pencil experiment demonstrates an idea that holds for all triangles.
Some might worry that the turning in step 4 is inconsistent with the other two actions of turning: here we are turning about the lead-tip of the pencil rather than the eraser end of the pencil.
To be consistent, in step 4 we could turn the pencil about the same eraser end too by sliding the pencil just past the vertex of the triangle and make use of the congruent vertical angles we noted in the last lesson.
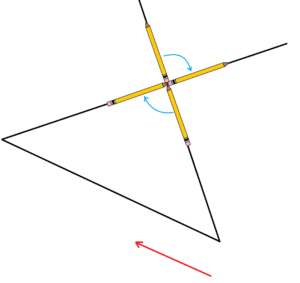
Turning on the tip or turning on the eraser applies the same amount of turning.
| Activity 1:
a) Draw a four-sided figure and apply the same pencil pushing idea to its interior four angles. Show that the four angles have measures that sum to two half turns, that is, add to \(360^{\circ}\).
b) Consider the following quadrilateral. Identify its four interior angles. Show that its four interior angles also have measures that add to two half-turns.
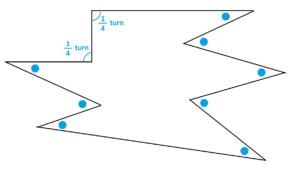
Activity 2: Explore the measures of the interior angles of five-sided figures. What can you say about the sum of those measures? (WARNING: A pencil inside a pentagon undergoes more than just a single half turn.) Activity 3: Draw a large 13-sided figure and use pencil-pushing to find the sum of the measures of its interior angles. How many half-turns? Activity 4: Find a general formula that seems to hold for the sum of measures of the interior angles of an \(N\)-sided figure. Activity 5: What can you say about the sum of measures of the (exterior) angles shown for this polygon? (See below too!)
Activity 6: What does pencil pushing say about the sum measures of the five angles in a lop-sided five-pointed star?
|
Comment: This animation from Magic Pi Animations is fun.

Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()

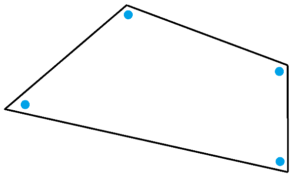

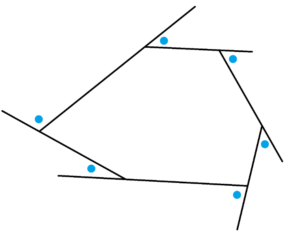
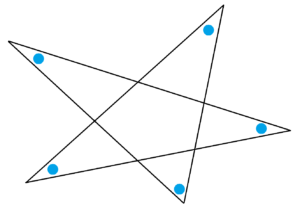 Question 7: Does the following polygon exist if we insist that all the angles marked with a blue dot are congruent, that is, have the same measure?
Question 7: Does the following polygon exist if we insist that all the angles marked with a blue dot are congruent, that is, have the same measure?