Here’s a famous puzzle.

You are brought to a crime scene. You are told that a thief just made off with a bag full of diamonds, escaping on a bicycle. You come across the following pair of bicycle tracks in the snow, no doubt made by the fleeing thief. But which way did the thief go?

Just by looking at the shapes of the tracks (tread marks and splashes of snow are inconclusive) can you determine which way the thieving cyclist went: left to right or right to left?

This charming curiosity appears in Joseph Konhauser, Dan Velleman, and Stan Wagon’s text Which Way did the Bicycle Go? … and Other Intriguing Mathematical Mysteries (MAA, 1996). They learned of the problem from a geometry course being developed at Princeton in the 1980s. This problem is also described in Sherlock Holmes novel, but Doyle, according to the three authors above, gives an incorrect (non-mathematical) solution for determining the direction of travel.

I usually present this puzzle as a group activity and guided discussion. To do so too, you will need the following supplies 

A bicycle

Yard Sticks/Meter Sticks

and if want to conduct the activity inside

Sidewalk chalk

About 40 feet of poster paper

Thick red markers and thick blue markers

Painter’s tape

Start by telling the story of the thief making off with a bag of diamonds while roughly sketching a pair of bicycle tracks on the board. Then ask

Does it make sense that there are two tracks? 

Answer: Yes! A bicycle has two wheels and each wheel leaves a track.

Now mention that your sketch is highly inaccurate, that we should work with a genuine pair of bicycle tracks in order to properly observe their mathematical structure.

Ask participants to cover each wheel of a bicycle with chalk, one wheel with blue chalk say, and the other red chalk. Roll out the poster paper in a corridor and ask a volunteer to ride a wobbly path down the paper roll (making sure to not head off the paper, but also to give a path with lots of left and right turns).

The chalk marks on the paper will likely be faint. Ask participants to draw over the colored traces with markers of the same colors.

Now bring the paper back into the room and hang it on the wall with painter’s tape. Ask folk to forget what they just witnessed and ask

Okay. You just came across these very tracks. Is it possible to determine which way the bicycle went?

(Of course, one can conduct this activity outside if you are able to ride a bicycle across a dirt ground, for instance, to make tracks.)

  

Two nudging questions

Ask these questions when/if frustration becomes too much.

Is it possible to say which track is most likely the back-wheel track and which is the front wheel track?

Answer: Think of how a bicycle is constructed. The front wheel of the bicycle can turn left and right, but the back wheel of a bicycle is fixed in its frame. This means that the more “stable” track is likely to be the back-wheel track and the wobblier one the front wheel track.

After some mulling time, next ask

You said that the back wheel is more “stable.” In what sense? What makes it stable? What else do you notice about the construction of a bicycle?

Hold up a bicycle. Observe that the back wheel is indeed fixed in its frame, but more is true.

i) The back wheel always points towards the point of contact on the ground of the front wheel, no matter which way the front wheel is pointing.

ii) The distance to that point of contact is fixed: it is the distance between the axles of the wheels.

This is usually enough to prod the group conversation to the solution. Participants might rephrase these two observations as

“So, each point on the back-wheel track points towards the front-wheel track at a fixed distance.”

Help guide everyone to a more precise description, something along the following lines.

“The tangent line at each point on the back-wheel track intercepts the front wheel track at a fixed distance.”

Hold up a yard stick as a tangent line at a point on the back-wheel track. Demonstrate that, in moving the along the back track, the tangent line does indeed intercept the front wheel track at some consistent fixed distance in one direction of motion but not in the other.

We have

For a given pair of bicycle tracks, it is not only possible to determine in which direction the bicycle traveled, but also the length of the bicycle that made those tracks!

Comment: Of course, we are presuming a mathematically ideal scenario here. As a bicycle turns left or right it tilts on its wheels and the points of contact to the ground shift to the side of the center-line of the wheels. Also, in riding a bicycle there are small degrees of slipping and sliding too. But despite these mathematical imprecisions, the technique described works extraordinarily well in practice! Next time you see mud tracks, water tracks, or sand tracks of a bicycle on the ground, examine them. You will be able to determine the direction of travel of the bike!

 

Here’s another picture of mathematically precise tracks. Here the cyclist rode in a loop.

In this picture, which is the back-wheel track? Which is the front-wheel track? Which way did the cyclist travel?

When Does the Method Fail?

 There are instances in which we cannot determine the direction of motion of the cyclist.

If the rider rides a perfectly straight path, the two tracks of the wheels overlap along a single straight line. It is impossible in this case to ascertain the direction of motion from analyzing the tracks.

What is another instance of rider motion for which one could not determine the direction of travel?

Answer:  A cyclist could ride in perfect circle.

It is worth pausing on this answer to ask: In this case, what do the two tracks look like? Can you still determine which track is the back-wheel track and which comes from the front wheel?

Because of the symmetry of the situation we cannot determine the direction of motion in this case too.

 

Here’s a surprisingly tough question.

1. Are these the only two cases in which we could not determine the direction of travel?

More precisely,

If a pair of smooth curves have the property that each tangent line to one curve always intercepts the other curve at two locations, a fixed distance either side of the point of contact along the tangent line, must the curves each have constant curvature?

Here are two more really tough questions.

2. Could two bicycles of different lengths produce the same pair of (non-straight) bicycle tracks?

3. Could a bicycle produce a single non-straight track? (That is, is it possible to ride a non-straight path on a bicycle so that back wheel track covers the front wheel track? Alternatively, could a bicycle and a unicycle produce exactly the same non-straight track?)

All three questions can be united as one.

 Could two bicycles of lengths \(r\) and \(s\) produce the same non-straight tracks?

Allow the cases \(s=-r\) and \(s=0\).

 

These questions are fun to explore, but they will require some technology help in order to draw bicycle tracks with the correct mathematical structure. (Write a set of parametric equations for a back-wheel curve, compute the unit tangent vector at a location on this curve and plot the endpoint of this vector.  The trace of this point is the front wheel track.)

It might be good to mull on these questions only a short while. The next part of the lesson continues the activity and brings matters back down to a manageable level.

 

Comment: A solution to Problem 3 appears in Dr. David Finn’s 2002 paper “Can a Bicycle Create a Unicycle Track?”. This question, along with question 1, is also discussed in Stan Wagon’s book Mathematica In Action: Problem Solving Through Visualization and Computation (Springer).  And the 2013 paper “Tractrices, Bicycle Tire Tracks, Hatchet Planimeters, and a 100-year-old Conjecture” by Robert Foote, Mark Levi, and Serge Tabachnikov explores the mathematics of tracks in great depth. 

 

THE AREA BETWEEN TRACKS

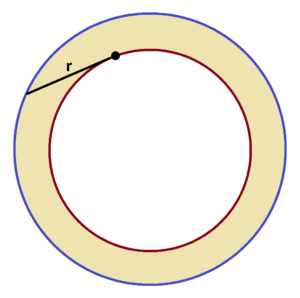
Let’s now attend to the goal of explaining why, after riding a complete loop, the area of the regions between the two tracks is sure to be \(\pi r^2\) where \(r\) is the distance between the two axles of the bicycle.

 

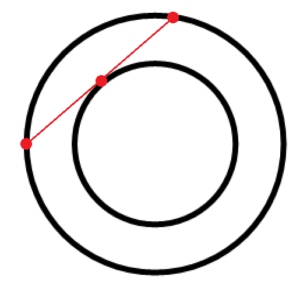
Optional Geometry Exercise:  Suppose a cyclist rides a perfect circle.

If you are familiar with basic circle theorems from geometry class and the Pythagorean theorem, you can prove that the area between the two circular tracks formed is sure to be \(\pi r^2\) no matter the size of the circles. How?

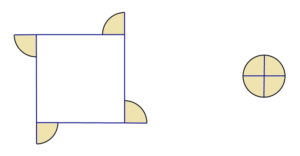
Let’s start by riding bicycles along loops that are a polygons!

Suppose we force the back wheel of the bicycle to follow a square path, pivoting on the back wheel at the corners and swinging the front wheel round. Can you see what with the front wheel path will look like? Can you see that the area between these tracks is, for sure, \(\pi r^2\)?

 

Think about rectangular back-wheel paths, triangular back-wheel paths, and other polygonal back-wheel paths.

For Consistency …

Let’s assume we’re always pushing the back wheel of a bicycle along a looped path in a counterclockwise direction. And to make sure the front wheel always stays on the outside of the loop, let’s assume we have a path that only makes left turns when we pivot on the back wheel. This means we’ll work with, just for now, convex shaped polygonal paths.

Our pencil-pushing work from lessons 1.3 and 1.7  now helps us out. We saw there that the measures of the exterior angles of a convex polygon always sum to one full turn, \(360^{\circ}\).

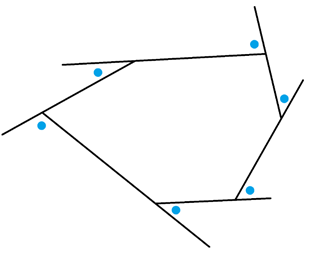
This allows us to conclude the following.

If we force the back wheel to follow a convex polygonal path, then the region between the front wheel and back wheel tracks is composed of a set of sectors of a circle of radius \(r\). Because the exterior angles of a regular polygon sum to \(360^{\circ}\), these sectors fit together perfectly to make one full circle.

Thus the area between the front-wheel and back-wheel tracks for a cyclist riding in a convex polygonal path is \(\pi r^2\).

EXPLORATION: Examine what happens for a cyclist riding a non-convex polygonal path. If you regard areas swept out in a counterclockwise direction as positive and areas swept out in a clockwise direction as negative, does it seem that the sum of positive and negative sector areas still make one full circle of positive area?

 

Smooth Curves

Any smooth convex curve can be approximated as a convex polygon by drawing short line segments between points of the curve. And if we ride the bicycle along the convex polygonal approximation, we know the area between the bicycle tracks approximating the original tracks is sure to be \(\pi r^2\). This approximates the area between the original pair of tracks.

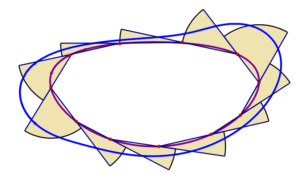
We can get a better approximation of the true area between the tracks by using a polygon to approximate the back-wheel track with many more sides composed of much shorter line segments. But we know that area between the tracks in this approximation will be too. We can do finer and finer approximations, but each time these approximations have value . Since the approximate values converge to the true value of the area between the original tracks, we can only conclude that the area between the original tracks must be \(\pi r^2\)too!

This does it for convex bicycle paths!

And if we develop a sufficiently robust theory of positive and negative area, one can indeed prove the general result. For any loop that has you turn a total of \(k\) full turns as you traverse it (for example, a “double loop” has \(k=2\), and figure 8 has \(k=0\)), the total area between the tracks, summing positive and negative areas, is sure to be \(k \times \pi r^2\).

 

Resources