Teacher’s Content PDF

STUDENT HANDOUTS

Welcome to a story about fractions, probability, and the infinite, all done through the deep play of garden walks!

Here’s how it goes:

Suppose 100 people walk down a garden path that leads to a fork. Those who turn to the left go to house A, those who turn to the right to house B. Let’s assume that there is a 50% chance that a person will turn one way over the other.

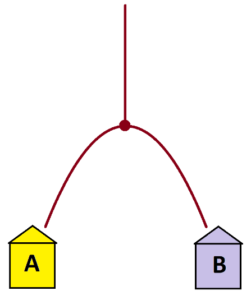
In this setup we’d expect roughly half the people, about 50, to end up at house A and about 50 to end up at house B. (It will likely not be exactly these numbers—the world isn’t perfectly predictable. Only in an ideal world we would expect precisely 50 people in each house.)

The following diagram of 100 people depicts this outcome.

The number 100 here is immaterial. The point is that if a square is used to denote the entire population of people walking down the path, then half the area of the square, designated A, represents half the count of people who ideally end up in house A and the other half of the area, designated B, represents half the count of people in house B.

This is the set-up of the game we shall play. Let’s now have some fun with garden paths!

 

Example: People walk down the following system of paths.

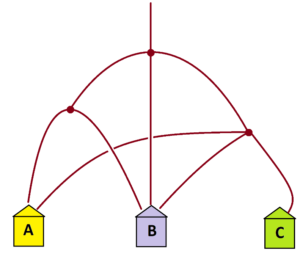
a) Which house do you think will end up with the most people in it? Which one the least?

Can you guess what fraction of people will end up in each house?

b) Use the square model to actually compute the fractions of people that end up at each house. (Assume that people arriving at each fork split equally in count in each direction.)

 

 

 Answer: At the first fork a third of the people go to the left, a third go straight, a third go to the right.

Of those who go to the left, half go to house A and half go to house B.

Of those who go straight, all go to house B.

Of those who go to the right, a third go to house A, a third go to house B, a third go to house C.

Do you see this information encapsulated in the following picture?

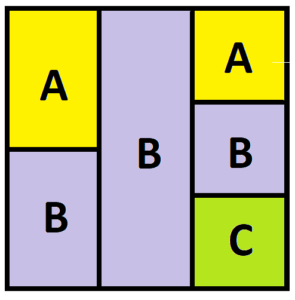
We see that the proportion of people who end up in house A is given as half of a third, that’s \(\frac{1}{6}\), plus a third of a third, that’s \(\frac{1}{9}\), giving the total proportion as \(\frac{1}{6}+\frac{1}{9}=\frac{5}{18}\).

The proportion of people who end up in house B is \(\frac{1}{6}+\frac{1}{3}+\frac{1}{9}=\frac{11}{18}\).

And the proportion of people who end up in house C has to be the remaining \(\frac{2}{18}\) (which is indeed the \(\frac{1}{9}\) we see in the picture).

Do these answers match your predictions from part a) of the question?

 

Question: Does it make sense to you that the three fractions we get add to \(1\)? Also, do you see that it is helpful not to simplify the fraction \(\frac{2}{18}\) in this example?

 

 

PEDAGOGICAL COMMENT: Many students have been trained to think that non-simplified fractions, such as \(\frac{2}{18}\) in this example, are inherently “wrong” and should not be left unmodified. A conversation that mathematics is not absolute and should be guided by context is appropriate here. Keeping all fractions in terms of eighteenths in this example allows us to readily compare proportions. For instance, we see that the counts of people all three houses follow a 5:11:2 ratio, with house B having more than double the count of people in house A, and so on.  

PEDAGOGICAL COMMENT: It can be difficult for younger students to draw free-form squares and rectangular areas within them. One can provide six-by-six grids to help. Some students might enjoy practice question 0 coming up next. (Warning: A count of 36 sub-squares is not good for all garden path systems as students will discover in practice question 3 of this lesson.) 

 

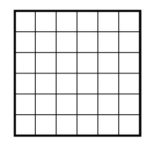
Practice 0: In each of the following examples determine the fraction of people that end up in each house.

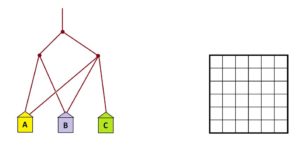
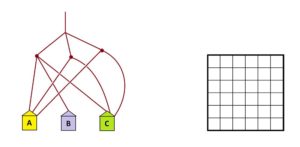
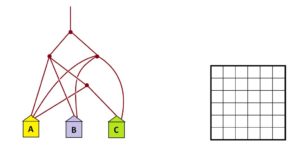
<All solutions appear in the Teachers’ Guide.>

 

Practice 1: A set of people walk down the following system of paths.

a) Any prediction as to which house will end up with the most people in it? The house that will end up with the least?

                              

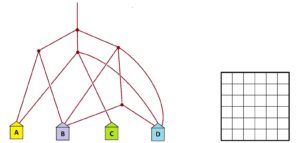
b) Show that the proportions of people who end up in each house are \(\frac{5}{18}\), \(\frac{6}{18}\), \(\frac{2}{18}\), \(\frac{5}{18}\)and , assuming that people arriving at a fork split themselves equally in count in each direction. (Surprisingly, equal proportions of people end up in houses A and D.)

We’ve provided here a six-by-six square to help with this question.

 

Practice 2: Answer the same questions for this garden path system.

                             

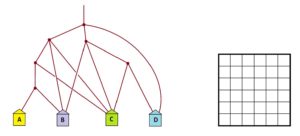
Practice 3: And answer the same questions for this garden path system. Here some forks have two paths that go to the same house.

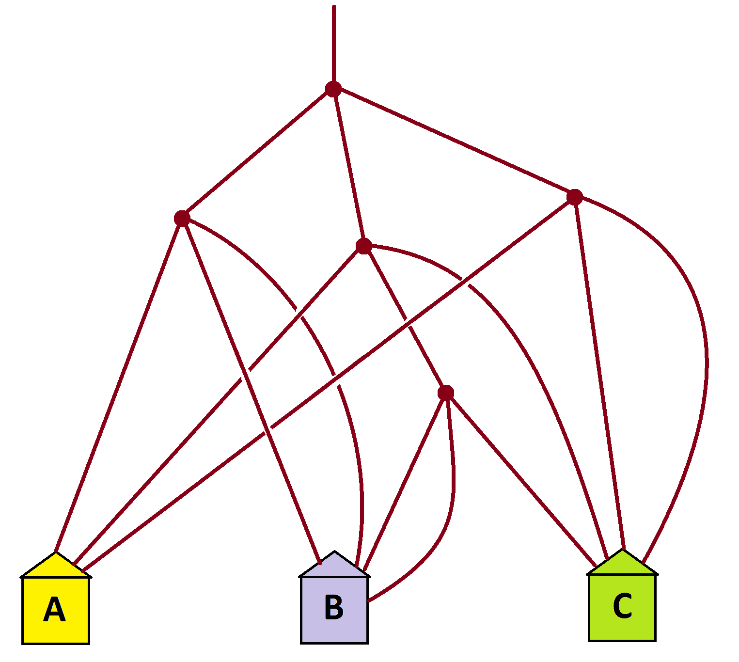
Practice 4: Design a garden-path system such that the house with least number of paths leading to it actually ends up with the most number of people in it.

 

Keep Going!

Have some fun making up your own garden path systems for others to solve. (Make sure you can solve them yourself!)

In your examples it might be best to use a blank square rather than one already divided into subsquares.

 

 

Resources