Garden paths are useful for analyzing the results of random actions. We’ll talk more deeply about probability theory in part II of these notes, but it is fun to see a hint of this application right now.

For the garden-path system we opened with—a single two-way fork—we could have people simply flip a coin to decide whether to turn to the left or to turn to the right when they reach that fork. About half the people will turn left and about half will turn right. (And, in an ideal world it would be exactly 50% turning each way.)

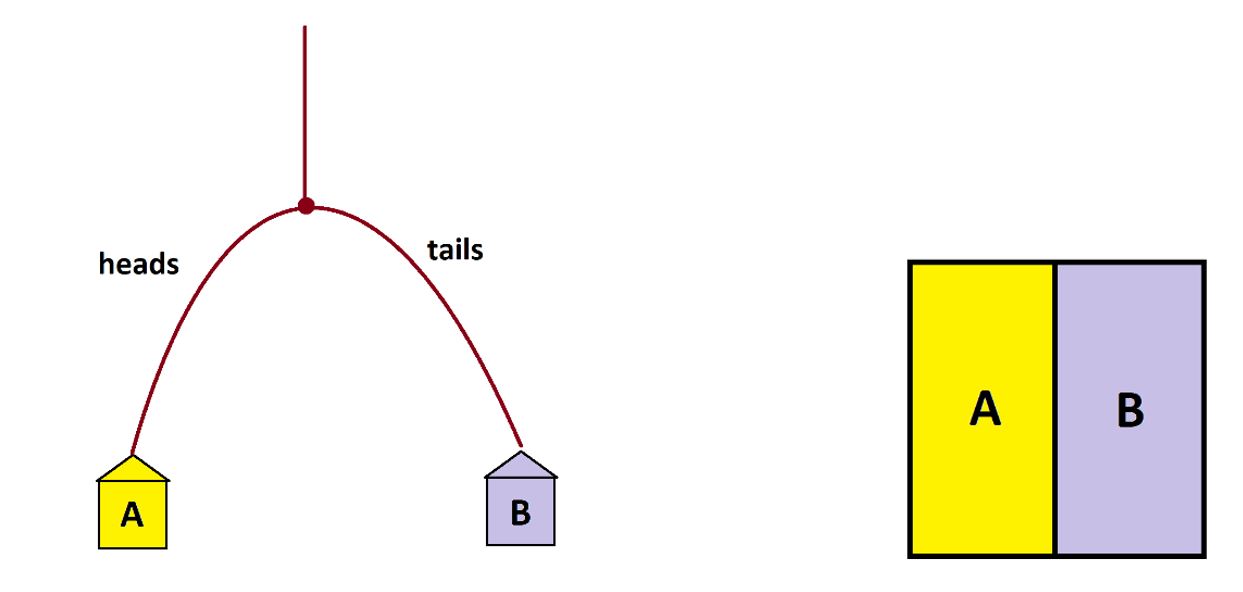
Or we could have people roll a die at the fork: If they roll an even number they turn to the left, to the right if they roll odd.

 

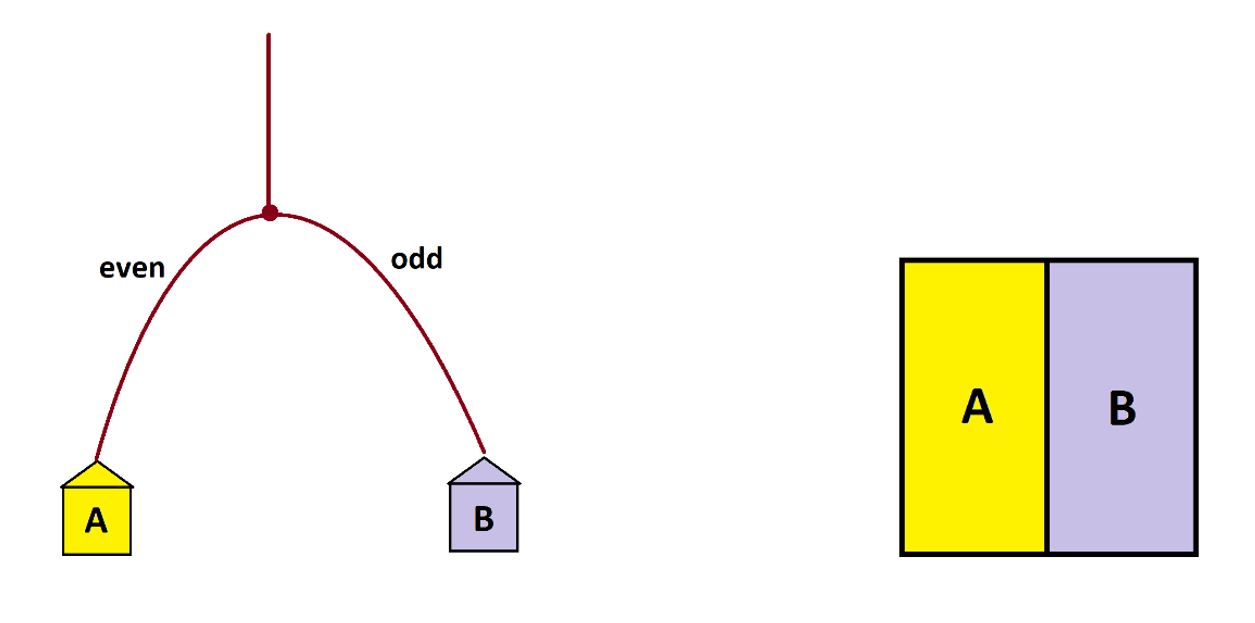
Or we could use the die to suggest a lopsided garden-path system based on rolls: rolling a 1 or 3 sends people to the left, say, with any other roll sending people to the right.

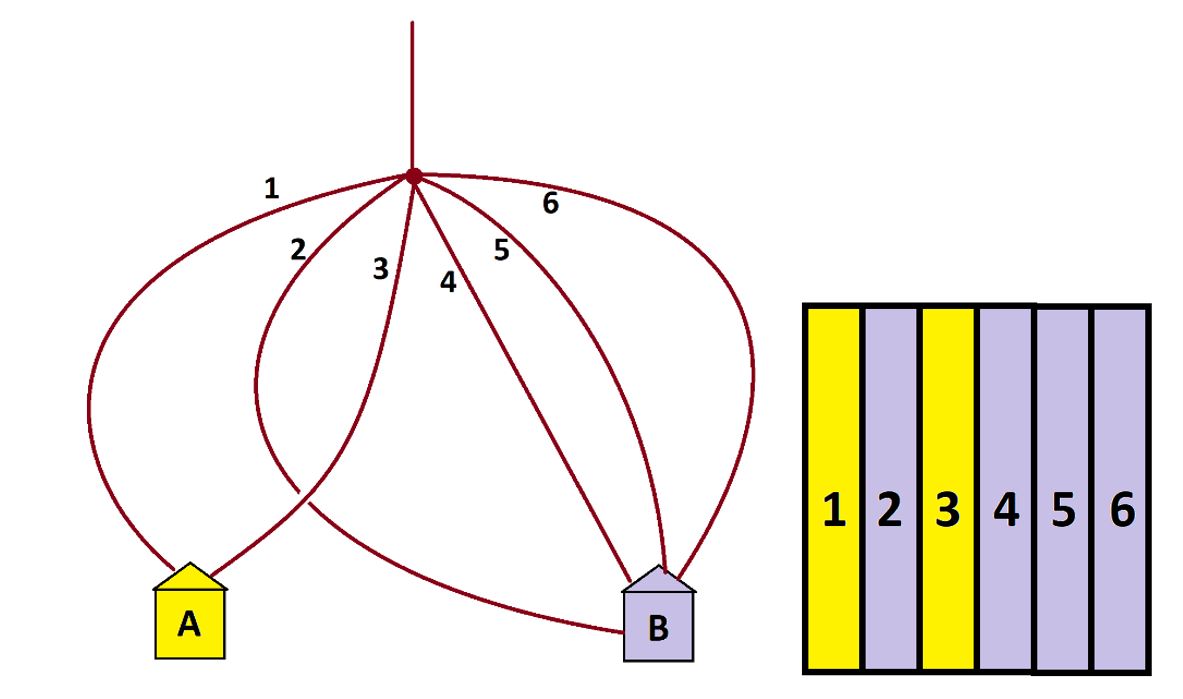
In this example we see that we expect about two-sixths, that is, one-third of the people will end up in house A and about two-thirds in house B.

 

Let’s make things more interesting and introduce some more forks.

 

Example: I toss a copper coin and then I toss a nickel coin. What are my chances of seeing a HEAD followed by a HEAD?

 

Answer: We can create a garden-path system that models this experiment of tossing two coins.

Let’s first have people arrive at a two-way fork and there they shall each toss a copper coin. If they get a HEAD, they’re good to keep going. But if they toss a TAIL, we’ll send them to the DON’T WANT house. (These folk are welcome to toss nickel coins too. But they are going to the DON’T WANT house no matter what!)

Let’s send those who keep going to another two-way fork. There they shall toss a nickel coin. Those who toss HEADS will go to the WANT house. Those who toss TAILS are off to the DON’T WANT house.

 

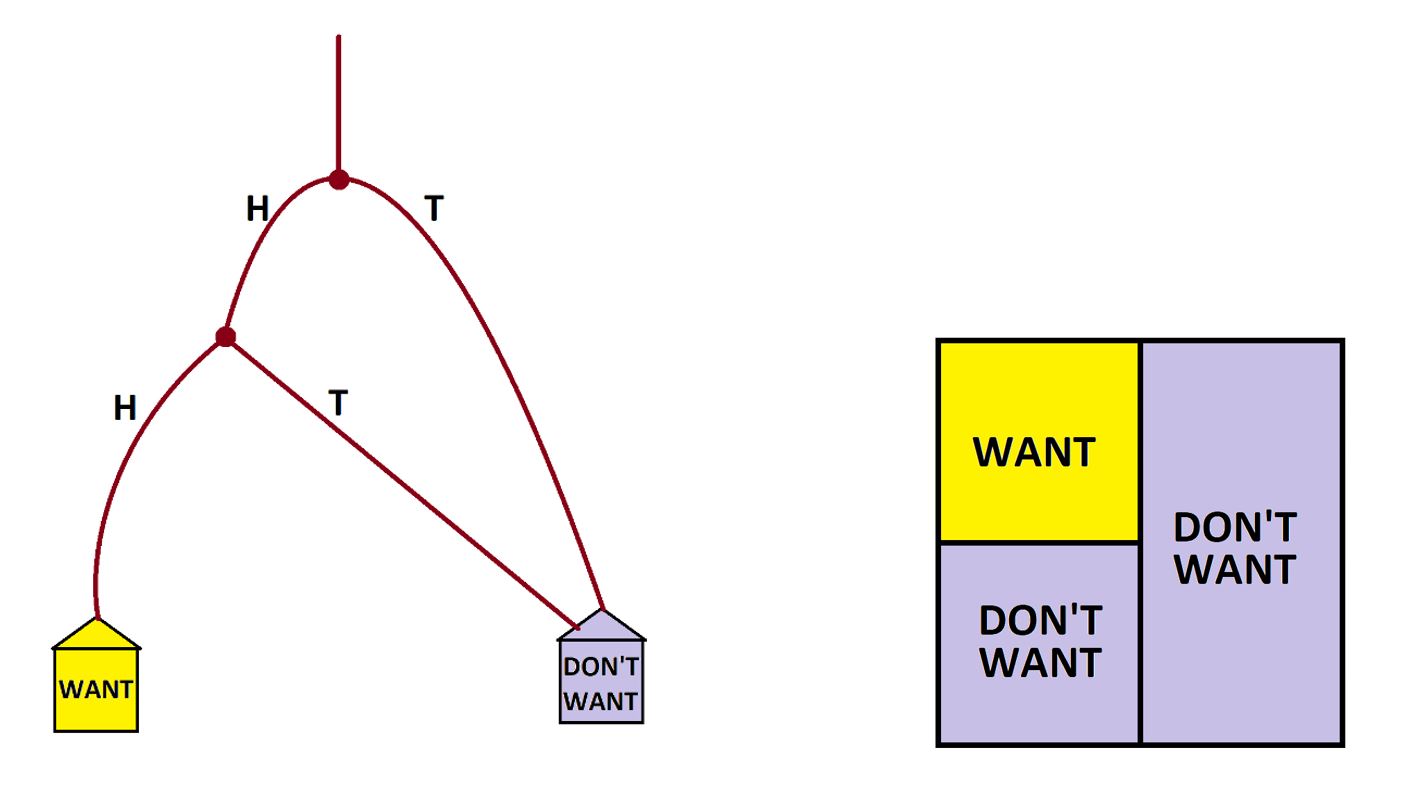
We see that we expect 25% of the people to get HEADS followed by HEADS.  That is, this thought experiment shows that the chances of tossing two heads in a row is 25%.

 

Example: I toss a copper coin, then I toss a nickel coin, and then I roll a die. What are the chances I shall see two HEADS and a 5 or a 6?

Answer: Can we create a garden-path system that models this three-step process? Sure!

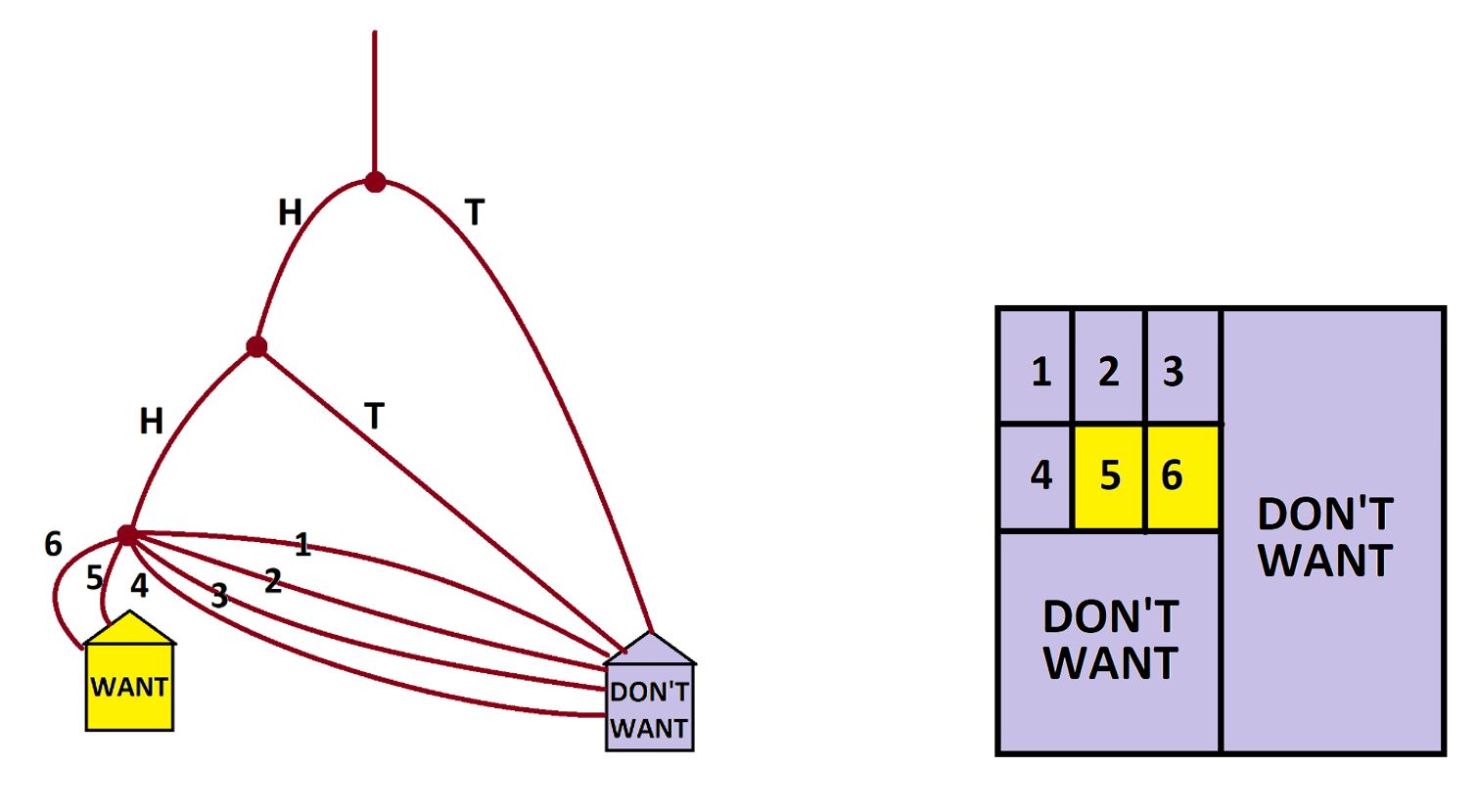
We see that two-sixths of one-quarter of the people who run through the system end up with the result we want. That is, the fraction \(\frac{2}{6}\times\frac{1}{4}=\frac{1}{12}\) of the people get two HEADS followed by a 5 or a 6. There is a one-in-twelve chance of seeing this outcome.

 

Example: A bag contains two red balls and three yellow balls. I pull out a ball at random, note its color, and put it aside. I then pull out a second ball at random from the four balls that remain in the bag and note its color too. What are the chances I see two red balls?

Answer: Here’s a garden path system, with one path at each fork for each ball in the bag that could be chosen.

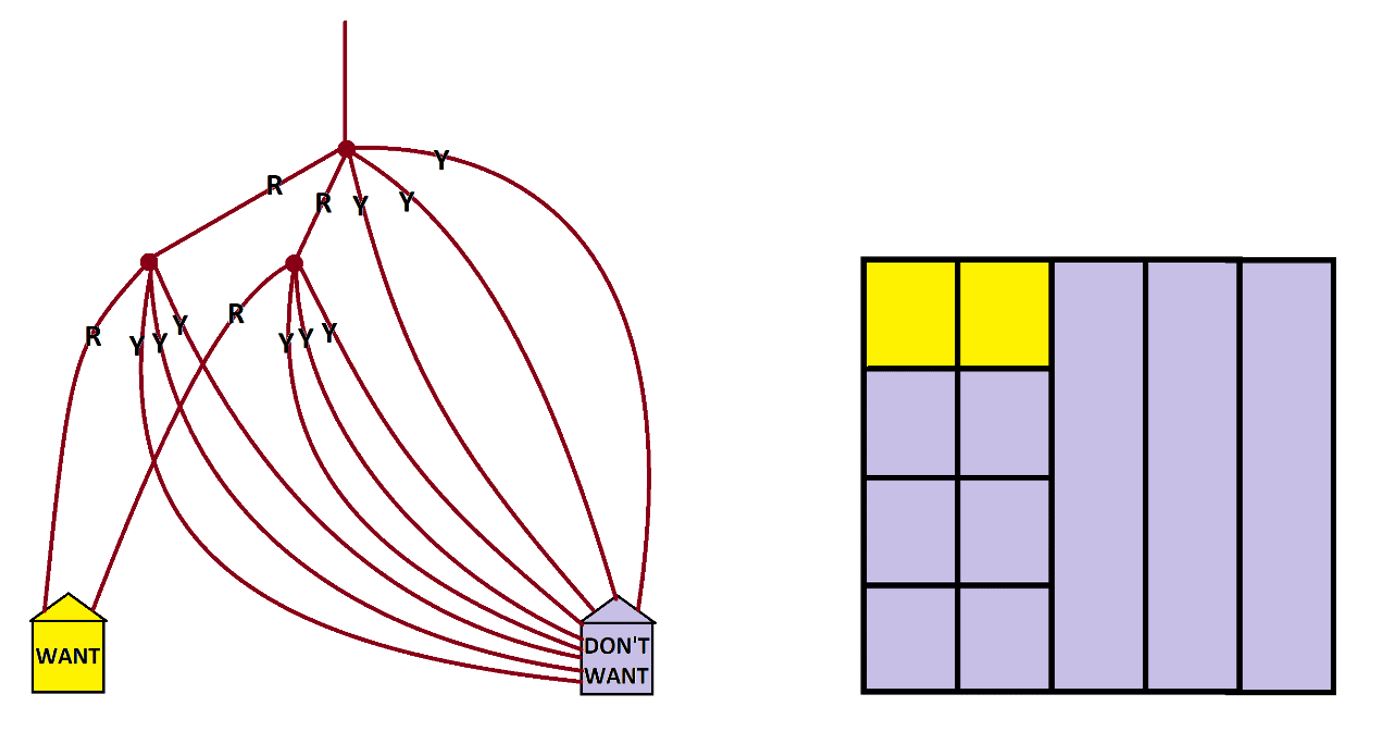
The chances of seeing two red balls is one-quarter of two-fifths (do you see that?). This is

\(\dfrac{1}{4}\times\dfrac{2}{5}=\dfrac{1}{10}=10%\).

 

Side Comment: It gets tedious drawing lots of paths for each and every individual option. Do you see that we could simplify the garden-path diagram by giving “weights” to each path? Turning to the left or to the right at each fork need not be equally likely: they could be some non-equal proportion. We can divide the square in these same proportions too.

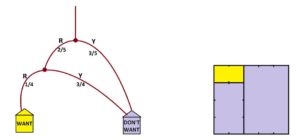
Here we see “one-quarter or two-fifths” more clearly.

 

PEDAGOGICAL COMMENT

Older students will typically make the suggestion to simplify diagrams by adding weights to the edges. Younger students might too if you make a “bit of a show” of how tedious it is to draw all six possible rolls of a die each-and-every time, for instance.

 

Side Comment: Some people like to draw garden-paths sideways and call them tree diagrams. They usually draw all possible forks and all possible options, making no judgement as to what is wanted and not wanted.

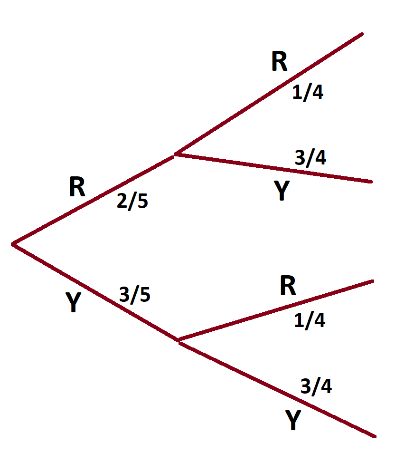
Practice 1: I roll a ruby die and then I roll an emerald die.

a) What are the chances that I will see an even number followed by a six?

b) What are the chances I will see only composite numbers on my rolls?

 

Practice 2: A bag contains two red balls and three white balls. I pull out a ball at random, note its color, and put it back in the bag. I then shake the bag with all five balls in it and pull out a ball again at random and note its color. What are the chances I see a red ball each time?

 

Practice 3: There is a 30% chance that I will sneeze at least once on any given day and a 60% chance I will yawn at least once.

a) What are the chances that I will both sneeze and yawn tomorrow?

b) What are the chances I will sneeze but not yawn?

c) What are the chances I will either sneeze or yawn but not both tomorrow?

 

<Answers appear in the Teacher’s Guide.>

 

Resources