The start of probability theory can, in one sense, be pinpointed to a single moment in time.

In 1654 French nobleman Chevalier de Méré wrote to prominent mathematician Blaise Pascal asking for advice on general “problems of points” (among other issues in making gambling bets). These problems go as follows.

Two friends each lay down $100 in a friendly “best of seven” tennis game, say. But rain interrupts play after just four games with one person having won three games and the other just one. How should the $200 in the pot be divvied between the two players so as to properly reflect the likelihood of each winning?

Pascal shared the question with colleague Pierre de Fermat. It is with de Méré’s inquiry that probability theory was born as a subject to be developed and deeply studied in its own right.

Comment: Italian mathematician Girolamo Cardano (1501-1576) worked with ideas akin to classical probability theory before this but did not publish his work. And, of course, gambling games have been in existence for centuries and scholars have wondered about, analyzed, and computed likelihoods of certain results. But the first definitive analysis of “chance” began with the work of Pascal and Fermat.

I invite you to think about and try to analyze de Méré’s problem. How would you approach it? What beginning assumptions would you make? What solution would you offer for splitting the pot between the two players and why?

Give this problem some thought yourself before reading the list of possible solutions my brain came up with.

Some Possible Solutions

Here are four possible ways to handle the problem-of-points conundrum.

Let’s start by giving the two players names: A for Albert and B for Bilbert, say, with A having won three games and B one.

Possible Solution 1: Just give each player back his $100 and play another day.

Possible Objection: A will likely complain that since he was on the verge of winning he should receive more than this amount.

Possible Solution 2: Give player A $150 and player B $50 to reflect the ratio of their wins thus far.

Possible Objection: A might argue that ratios are unfair. For example, if he were to win the next game, he’d be given the full $200 and player B $0, which is more than what the 4 win-to-1 win ratio would suggest ($160 and $40). Ratios undercut what A deserves!

Possible Solution 3: Analyse the problem with Garden Paths.

Suppose A and B are equally strong players, each just as likely to win any particular game. Here is the garden path analysis under this assumption.

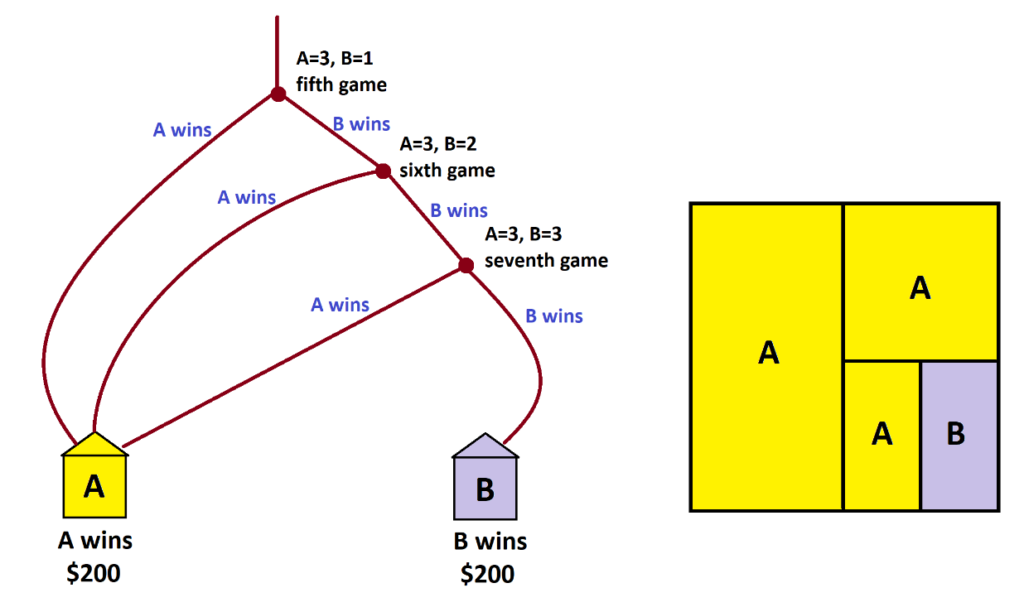
We see in this scenario that B has a one-eighth chance of winning the pot. This suggests splitting the pot in a 7:1 ratio, which corresponds to giving A $175 and B $25.

Possible Objection: A would argue that the evidence from the first four games played (three wins for A, one for B) suggests he is the stronger player, beating B not just 50% of the time but actually 75% of the time.

Possible Solution 3: Analyse the problem with weighted Garden Paths, assuming A has a 75% chance of winning any particular game.

This gives the following diagram.

We see in this scenario that B has only a one in sixty-four chance of winning the pot. This suggests the split $196.875 for A and $3.125 for B. (How should the handle the split one-cent?)

Possible Objection: B claims that he was “laying low” for the first few games to give A a false sense of confidence. He actually has a 95% chance of winning any given game and was going to come in strong for the next three games.

Challenge: Find yet another reasonable solution to de Méré’s challenge.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources