Global Math Project Experiences
2.7 ASIDE: Does “and” mean “multiply” in Probability Theory? (PART II)
Lesson materials located below the video overview.
Consider this example.
Suppose I roll a die and then flip a coin. What are the chances that I see a SIX followed by a HEAD?
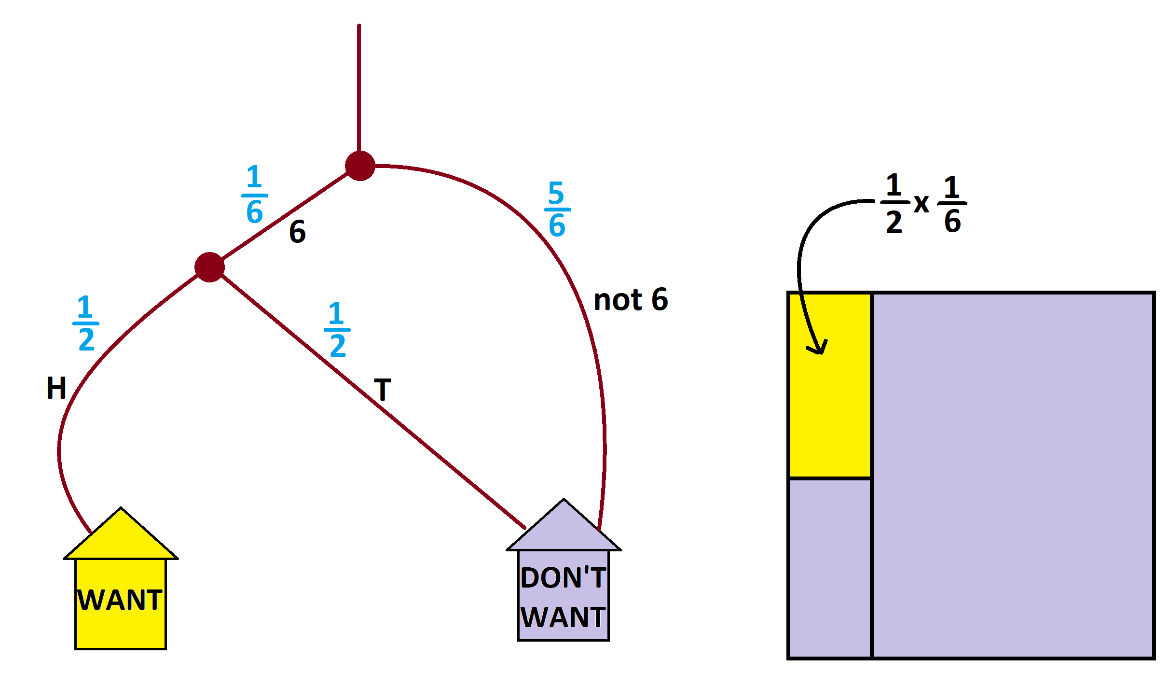
Let’s draw a (weighted) garden path system for this problem.
At a first fork people roll a die. Those who roll a 6—and we expect one-sixth of them to do so—continue on and those that don’t will head to the DON’T WANT house. (They are welcome to toss coins too, but they are heading to that house no matter what.) Those who continue reach another fork at which they flip a coin with those getting HEADS heading to the WANT house and those getting TAILS to the DON’T WANT house.
We see that half of one-sixth of the people in this system end up in the WANT house.
We have
\(P\left(\text{SIX and then HEAD}\right)=\dfrac{1}{2}\times \dfrac{1}{6}=\dfrac{1}{12}\).
So, naively, it seems that we have simply multiplied together two basic probabilities: the chances of rolling a SIX with a die, \(P\left(SIX\right)=\frac{1}{6}\), and the chances of flipping a HEAD with a coin, \(P\left(\text{HEAD}\right)=\frac{1}{2}\) .
And this appears to be the correct thing to do when we look at the area picture for the garden path system: we identified a desired fraction of a fraction of the whole square, namely, one half of one sixth of the square.
These observations are, of course, valid and correct. But there is a subtlety glossed over in playing with a coin: no matter which population of people flip a coin—those who have just rolled a SIX on a die, those who just rolled a THREE, those who never rolled a die at all—we expect half of that population to get a HEAD. Always half. A coin does not “care” what previous actions you may have just performed nor the results you got from them.
But some actions have outcomes whose chances of occurring do depend on what might or might not have occurred just beforehand.
We have already seen this phenomenon with an example from lesson 2.2.
Example: A bag contains two red balls and three yellow balls. I pull out a ball at random, note its color, and put it aside. I then pull out a second ball at random from the four balls that remain in the bag and note its color too. What are the chances I see two red balls?
Here’s the weighted garden path system for the example.
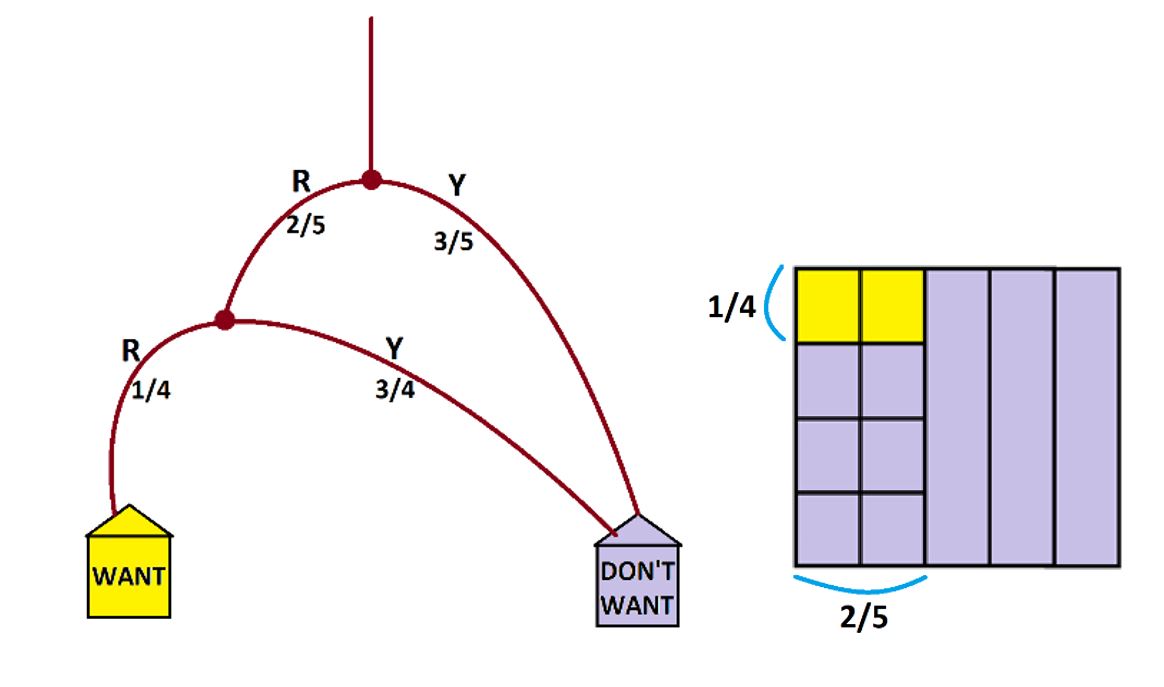
At the first fork people pull out a ball from a bag containing two red and three yellow balls. We expect two-fifths of them to pull out a red ball.
\(P\left(\text{RED}\right)=\dfrac{2}{5}\)
Those who pull out a red ball go on to a second fork where they are asked to pull out a ball again. But the probability of pulling out a red ball has changed because of the action that just occurred: there are now only four balls in the bag of which only one is red.
\(P\left(\text{RED, given that you previously pulled a red ball}\right)=\dfrac{1}{4}\)
The proportion of people who pull out two red balls is one-quarter of two-fifths of the folk
\(P\left(\text{RED, and then RED}\right)=\dfrac{2}{5}\times \dfrac{1}{4}=\dfrac{1}{10}\),
which is the product of two individual probability values, but with the second one is a value calculated in the context of having just seen a previous outcome.
Notation and Jargon: Suppose one is in the midst of performing two actions and that we have just seen outcome \(A\) from the first action. Suppose we are hoping to see outcome \(B\) from the second. People write \(P\left(B |A\right)\) for probability seeing outcome \(B\) in the second action under the assumption we have just seen outcome \(A\). This is read as the “probability of \(B\) given \(A\)” and is called a conditional probability: it is the probability of seeing outcome \(B\) under the circumstance (condition) you have just witnessed outcome \(A\).
For instance, in our example of pulling out balls from a bag one after another, we have
\(P\left(\text{second ball RED | first ball RED}\right)=\dfrac{1}{4}\).
And for practice, can you see that
\(P\left(\text{second ball YELLOW | first ball RED}\right)=\dfrac{3}{4}\),
\(P\left(\text{second ball YELLOW| first ball YELLOW}\right)=\dfrac{1}{2}\), and
\(P\left(\text{third ball RED | first and second balls YELLOW}\right)=\dfrac{2}{3}\)?
Working abstractly, consider a double-barreled experiment where we are hoping to see outcome \(A\) from the first experiment, followed by outcome \(B\) from the second. In a garden path system we expect fraction \(P\left(A\right)\) of the people to first see outcome \(A\). Of those people who get this outcome, we then expect fraction \(P\left(B | A\right)\) of them to see outcome \(B\) from the second experiment. Thus the fraction of people we expect to see is the fraction of a fraction \(P\left(B | A\right) \times P\left(A\right)\) of the people.
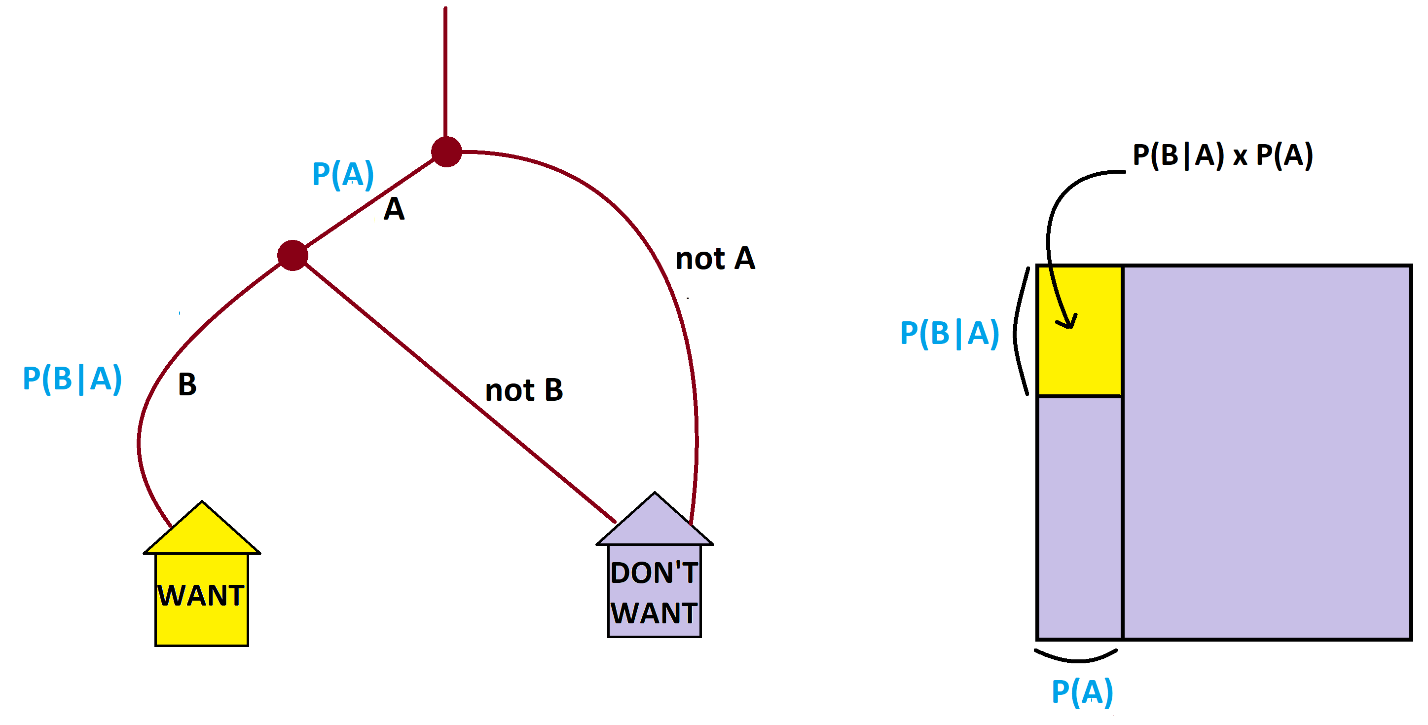
So here then is what people actually mean when they say that “and means multiply” in probability theory.
THE MULTIPLICATION PRINCIPLE IN PROBABILITY THEORY
Suppose one performs one task in hopes of getting outcome \(A\), and then performs a second task in hopes of getting outcome \(B\). To work out the probability of seeing \(A\) and then \(B\), that is, \(P\left(A \> \text{followed by} \> B\right)\), work out:
\(P\left(A\right) = \) the probability of seeing outcome \(A\) in running the first task alone,
\(P\left(B|A\right) =\) the probability of seeing outcome \(B\) in the second task under the assumption you have indeed just seen outcome \(A\) in the first.
Then
\(P\left(A \> \text{followed by} \> B\right) =P\left(A\right) \times P\left(B|A\right)\).
This product is the product of probabilities you see along the path to the WANT house if you work with a weighted garden-path diagram.
This principle is confusing when using examples of rolling die and flipping coins: the subtlety of conditional probability is hidden. As we mentioned, coins, for instance, do not “care” whether or not you have previously rolled a die: \(P\left(\text{HEAD | 6}\right)\) is just the same as \(P\left(\text{HEAD}\right)=\dfrac{1}{2}\) and one might not notice a conditional probability at play.
Jargon: Two actions or experiments are said to be independent if, in running the two actions one after the other, in either order, the outcome of the first action in no way influences or affects the outcomes of the second.
For example, rolling a die and flipping a coin are independent actions.
Me choosing a pair of trousers to wear from my wardrobe at random and me choosing a shirt to wear are not independent exercises: if I happen to pull out my purple trousers first, then I will make sure I avoid choosing a purple shirt. Thus the outcome of choosing trousers might well influence my choice of shirt.
If for two experiments we are hoping to see outcome \(A\) from the first experiment and then outcome \(B\) from the second, then \(P\left(B|A\right)\) is the probability of seeing this happen. But if the second experiment is independent of the first, then the chances of seeing outcome \(B\) under the condition you have just seen outcome \(A\) should be no different than just seeing outcome \(B\), in general. For independent events, we have \(P\left(B|A\right)=P\left(B\right)\).
For example, in rolling a die and flipping a coin \(P\left(\text{HEAD | 6}\right)=P\left(\text{HEAD}\right)=\dfrac{1}{2}\).
One has to use one’s own judgment and common sense to decide whether or not two (or more) experiments are independent.
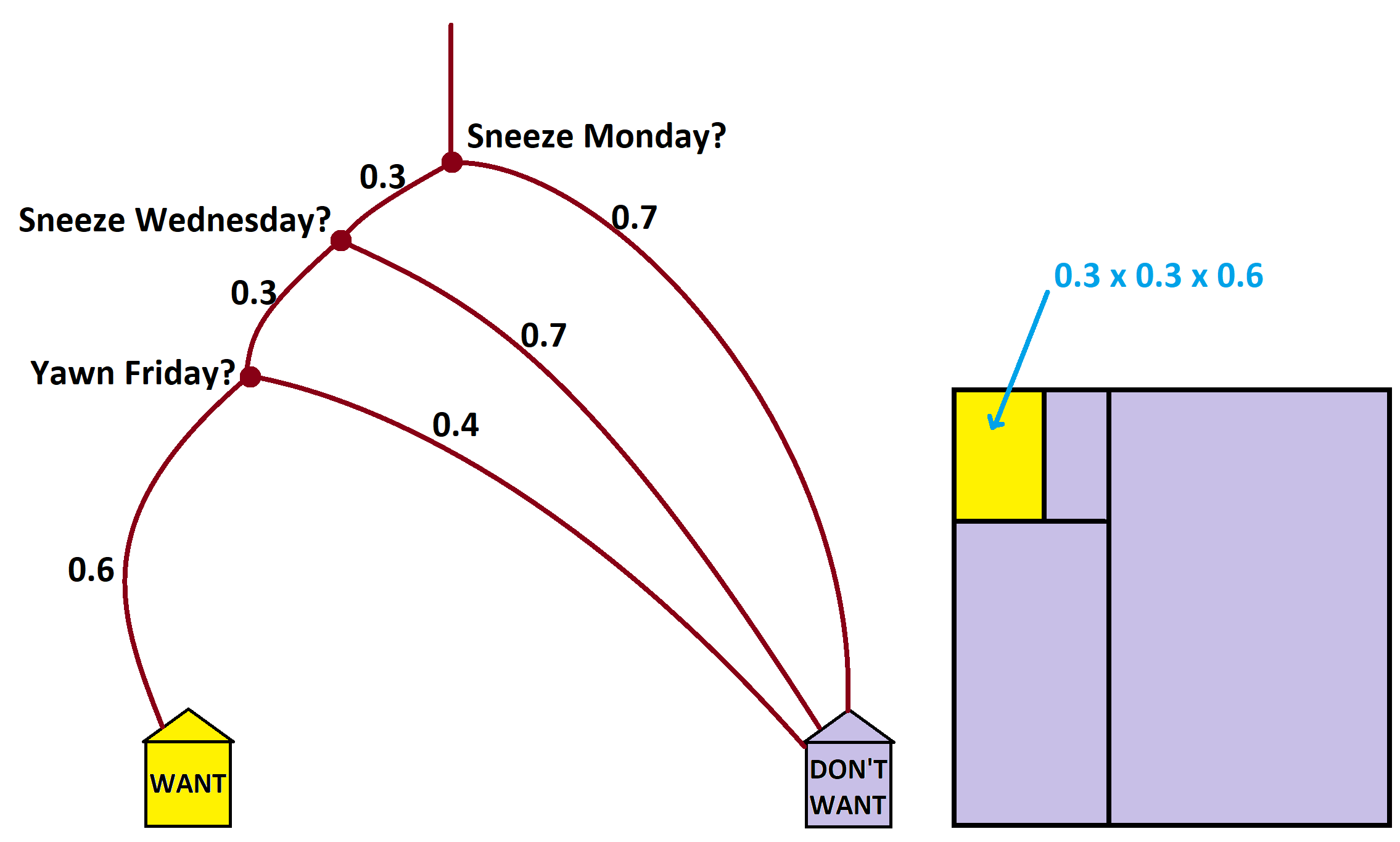
Example: On any given day there is a 30% chance that I will sneeze at least once and a 60% chance I will yawn at least once. What are the chances that, next week, I will sneeze at least once on Monday, sneeze at least once on Wednesday, and yawn at least once on Friday?
Answer: Let \(P\left(sneeze\right)\) and \(P\left(yawn\right)\) denote the probabilities of sneezing and yawning at least once, respectively, on any particular day. We have
\(P\left(sneeze\right)=0.3\)
\(P\left(yawn\right)=0.6\).
The information in the question seems to imply that sneezing on any particular day is no way dependent on whether or not I sneezed on a previous day nor on whether or not I yawned. Similarly, the chances of me yawning at least once on any particular day seem to be independent of any other factors.
So
\(P\left(\text{Sneeze on Wednesday}|\text{Sneezed on Monday}\right)\) is \(0.3\) as well, the general probability of sneezing,
and
\(P\left(\text{Yawn on Friday}|\text{Sneezed on Wednesday & Sneezed on Monday}\right)\) is \(0.6\), the general probability of yawning.
Thus the probability we seek is the product of probabilities
\(P\left(\text{Sneeze Monday, and then Sneeze Wednesday, and then yawn Friday}\right)= 0.3\times 0.3 \times 0.6 = 5.4\%\)
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


