Global Math Project Experiences
2.6 ASIDE: The Infamous Two-Girls Paradox (PART II)
Lesson materials located below the video overview.
Here is a famous puzzle that has befuddled the best of mathematical minds. It snagged me too when I first thought about it.
Consider three scenarios.
Albert, who you just met, tells you that he is the father of two children and that his oldest child is a girl. What are the chances that his other child is also a girl?
Bilbert, who you just met, tells you that he is the father of two children and that one of his children is a girl. What are the chances that his other child is also a girl?
Cuthbert, also a new acquaintance, tells you that he is the father of two children and that one of his children is a girl who was born on a Tuesday. What are the chances that his other child is also a girl?
Believe it or not, the usual answers presented are, in turn, \(\frac{1}{2}\), \(\frac{1}{3}\), and \(\frac{13}{27}\), which are mighty strange, and hence paradoxical! “Surely the answer is 50% in each and every case?” most would cry, figuring that there is a fifty-fifty chance for the unmentioned child to be one gender or the other! “The additional information supplied in the latter two cases is surely extraneous and immaterial?”
The trouble is that one can legitimately argue the standard answers are incorrect! This then supplies a paradox within the paradox, the feature that snags professionals too!
Let me explain the standard answers and why they should be challenged.
We’ll assume that giving birth to a child of any particular gender is indeed 50%.
Question 1: Is this indeed the case? What do world statistics seem to say for the percentage of girls born each year versus the percentage of boys?
Let’s suppose we encounter a large number of fathers, each with two children, say, 1960 of them. (I admit this is a strange number to pull out of the air! You’ll see as you read on that I realized that having a number divisible by seven a couple of times – there are seven days of the week—and divisible by two a couple of times—there are two genders—turns out to keep the numbers friendly.)
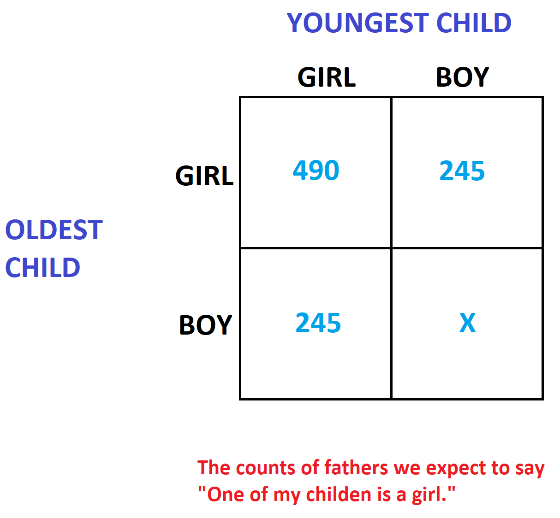
Among the 1960 fathers we encounter we expect half of them, that is, 980 of them, to have oldest child a girl. Of those 980 fathers, we expect half of them, that is 490 of them, to have youngest child a girl and half of them to have youngest child a boy. Similarly, of the 980 fathers we expect with oldest child a boy, half will have second child a girl and half second child a boy.

Albert tells you that he is among the 980 fathers with oldest child a girl (first row). The chance that he is actually among the subset of 490 fathers with youngest child also a girl is \(\dfrac{490}{980}=\dfrac{1}{2}\).
But a rub comes with Bilbert: we are not told which child he commented on nor the mechanism or motivation which caused him to mention the gender of a particular child. Maybe he just picked one of his two children at random and mentioned the gender? Or perhaps he lives in a society that requires you to mention having a female child if you legitimately can? Just these two different motivations already give two different values for the chance that Bilbert’s second child is also a girl.
Let’s analyze the probabilities under the effect of each of these motivations.
Motivation 1: Let’s assume each father of two children secretly flips a coin to choose a child whose gender he will divulge.
Looking at the table above we see that there are 980 fathers with a child of each gender and after flipping a coin we expect half these, \(245+245=490\) of them, so say “One of my children is a girl.” There are also 490 fathers with two girls who will say “One of my children is a girl” for sure. Bilbert tells us that he is among the fathers who say these words. The chances that he is a father of two girls is thus \(\dfrac{490}{980}=\dfrac{1}{2}\).
Motivation 2: Each father lives in a society that requires you to mention having a female daughter if you legitimately can.
There are now \(490 \times 3 = 1470\) fathers who, for sure, will say to you “One of my children is a girl.” The chance that Bilbert is among the sub-group of fathers with two girls is \(\dfrac{490}{1470}=\dfrac{1}{3}\).

Practice 1: Suppose Bilbert lives in a society that requires you to mention that you have a male child if you legitimately can. Given that Bilbert said “One of my children is a girl,” what now are the chances that Bilbert has two girls?
The situation with Cuthbert is analogous, just a little more detailed.
We need to consider girls born on a Tuesday (let’s assume one-seventh of any given count of babies are born on any given day of the week). We also need to consider girls not born on a Tuesday and consider boys. The following table captures the appropriate counts for a group of 1960 fathers.

Motivation 1: Let’s assume each father of two children secretly flips a coin to choose a child whose gender he will divulge, along with the day of the week the child was born.
There are \(60+70+60+70= 260\) fathers with just one female child born on a Tuesday and, after flipping a coin, we expect half of them, \(30+35+30+35=130\) of them, to say the words “One of my children is a girl born on a Tuesday.” There are \(10\) fathers with two girls each born on a Tuesday who will say these words for sure. So we expect a total of \(140\) fathers will make this comment.
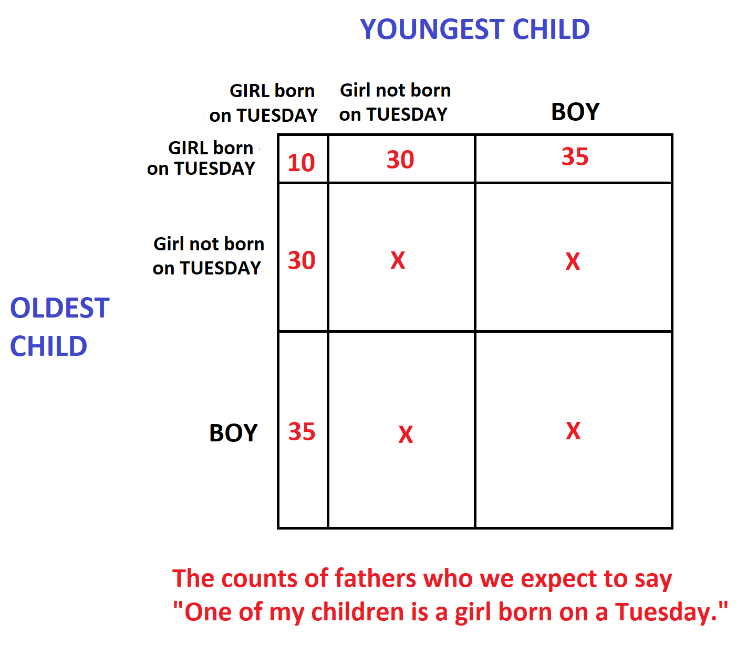
Of those 140 who say these words, we see that \(30+30+10=70\) of them have second child a girl. Thus the chances that Cuthbert is among this special set of father is \(\dfrac{70}{140}=\dfrac{1}{2}\).
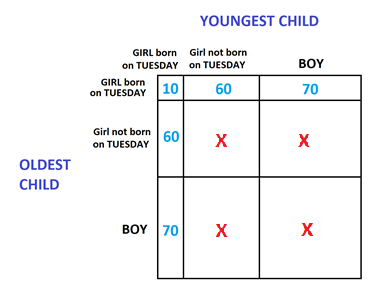
Motivation 2: Each father lives in a society that requires you to mention having a female daughter born on a Tuesday if you legitimately can.
We see that there are \(10+60+70+60+70=270\) fathers who will be sure to mention that they have a girl child born on a Tuesday. Of these, there are \(10+60+60=130\) fathers having a second child a girl. The chance that Cuthbert has two daughters is thus \(\dfrac{130}{270}=\dfrac{13}{27}\).
Practice 2: Suppose Cuthbert lives in a society that requires you to mention that you have a male child if you legitimately can. Given what Cuthbert said what are the chances that Cuthbert has two girls?
Practice 3: Suppose Cuthbert lives in a society that requires you to mention that you have a female child if you legitimately can. Further, assume people like to add the day of the week their daughters were born and when given a choice between two daughters to mention, they use the flip of a coin to decide. Given what Cuthbert said what are the chances that Cuthbert has two girls?
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


