Infinite garden paths are just terrific for analyzing (potentially) infinite probability experiments.

 

Consider this question.

 

I will repeatedly toss a coin. What are the chances that I will see two heads tossed in a row (HH) before I’ll see a head immediately followed by a tail (HT)?

 

We can answer this question with pure logic.

Answer 1: If I first toss a tail or two tails or a string of tails of any length, I am no closer to seeing either HH or HT. This experiment doesn’t “kick in” until I see my first head. Once I do, there is a 50% chance I’ll see a head after that (to get HH) and a 50% chance I’ll see a tail (to get HT). Thus there is a 50% chance I will see HH first.

 

But we can also analyze this question by setting up a garden path system to model it.

Attempt Answer 2: Imagine an inconceivably large number of people each about to repeatedly toss a coin. They all begin in the state “about to toss their coin for the first time,” which we’ll label S.

On the first toss, some will toss a head (half of them in an ideal world) and be set for seeing either HH or HT. The other half will toss a tail, which is irrelevant to the outcome desired. We may as well send those folk back to the start state and have them try again.

Of those who first toss a head, half (in an ideal world) will toss a head again to see HH and half a tail to see HT.

We see now that having this inconceivable large set of people each repeatedly toss a coin is equivalent to sending this set of people through a system of garden paths that looks like this.

 

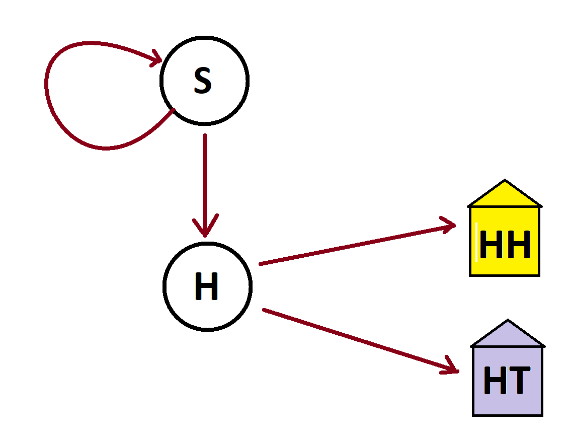
This garden path system has a path that loops back to the node from which it came.

But everyone sent back to start will (eventually) toss a HEAD and move through the system. (What is the probability that someone will toss a TAIL infinitely many times in a row?) So, philosophically, this system of garden paths is equivalent to one without the loop back to start.

And indeed we see that 50% of the people running the experiment will see HH first and 50% will see HT first.

EXAMPLE: A Dice Roll Question

I will repeatedly roll a die. What are the chances that I will see the roll of a 1 and the roll of a 2 before I ever see a roll of a 6?

 

To answer this question, imagine an inconceivably large number of people each rolling a die repeatedly. When folk get going, some will see both the roll of a 1 and a 2 before seeing a 6. Others won’t. We want to know the proportion of people that do.

Everyone begins at a start state, about to start their rolls.

Some will roll a 6 right away—one sixth of them in an ideal world—and will be immediately rules out.

Some will roll a 3, 4 or 5—one half of them in an ideal world. As none of these numbers is relevant to what we are examining they will roll again as though they are starting from the beginning of the experiment again.

Some will roll a 1 or a 2 right away—one third of them in an ideal world—and will still be “in the game.”

Of those in the last group …

Some will roll a 6 on the next roll—one sixth of them in an ideal world—and will be ruled out.

Some will roll a 3, 4, or 5—half of them in an ideal world—which would be considered an irrelevant roll and so will remain in the same predicament. So too will rolling a repeat 1 or a repeat 2, which will happen—in an ideal world—for one sixth of the people. In total, then, \(\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\) of these people will have an irrelevant roll and be back in the same state.

The remaining folk—one sixth of them in an ideal world—will get what they are looking for, either a 1 if they earlier rolled a 2, or a 2 if they earlier rolled a 1.

The following system of garden-paths encapsulates the relationships between all these possible states.

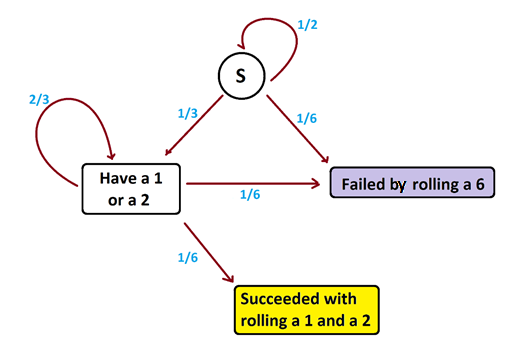
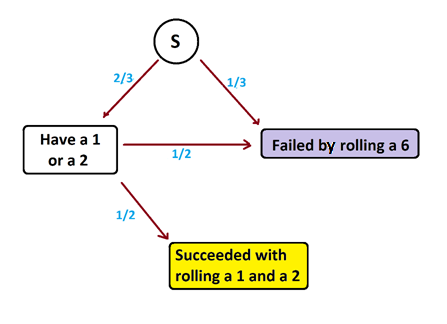
But if we are only interested in the proportions of folk ending up in each final state (and not the expected number of steps to each a final state), we can ignore loops! Taking into account the weights on the various edges we see that this system is equivalent to the following system. (Make sure you understand the weights on edges you see in this second diagram.)

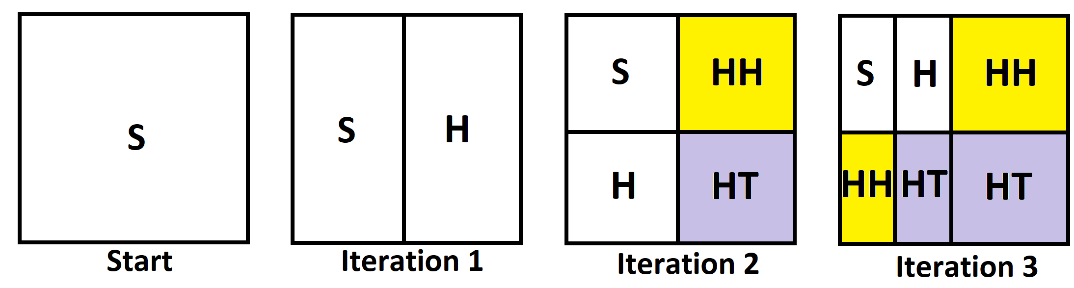
This gives the following area diagrams

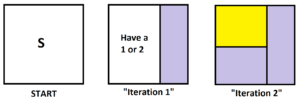
from which we conclude that the probability of seeing both the roll of a 1 and a 2 before seeing the roll of a 6 is \(\dfrac{1}{2} \times \dfrac{2}{3}=\dfrac{1}{3}\).

 

Practice Problem 1: I will repeatedly roll a die. What are the chances that I will see either the roll of a 1 or the roll of a 2 before seeing a roll of a 6?

 

Practice Problem 2: I will repeatedly roll a die. What are the chances that I will see the roll of a 1 and a roll of a 2 and a roll of a 3 before seeing a roll of a 6?

 

 

Example: A Coin Tossing Question

I will repeatedly toss a coin. What are the chances that I’ll see three consecutive heads (HHH) before I see a head-tail-head triple (HTH)?

Here is a garden path diagram modeling runs of this experiment. Each edge has equal weight of a half. (Did I get the diagram right?)

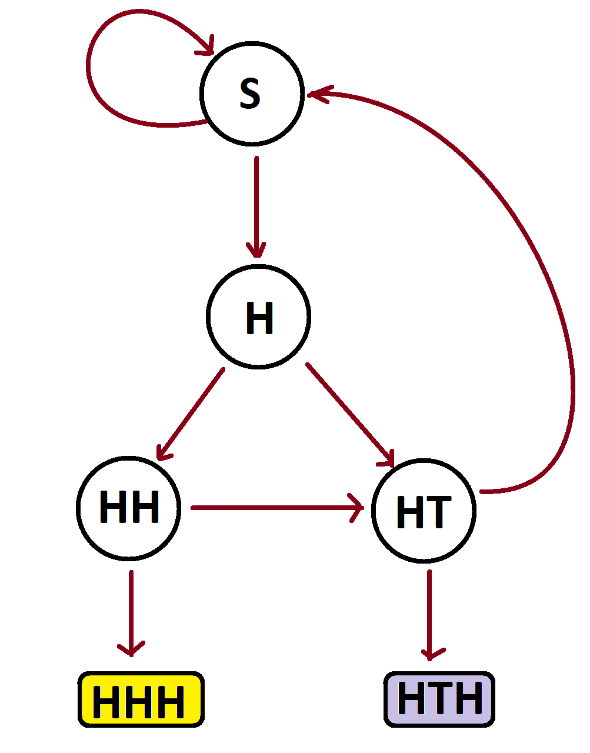
As we are only interested in the proportion of times we end up in each final state, we are permitted to ignore loops. So in this context this system is equivalent to the diagram:

This leads to the following area-model diagrams.

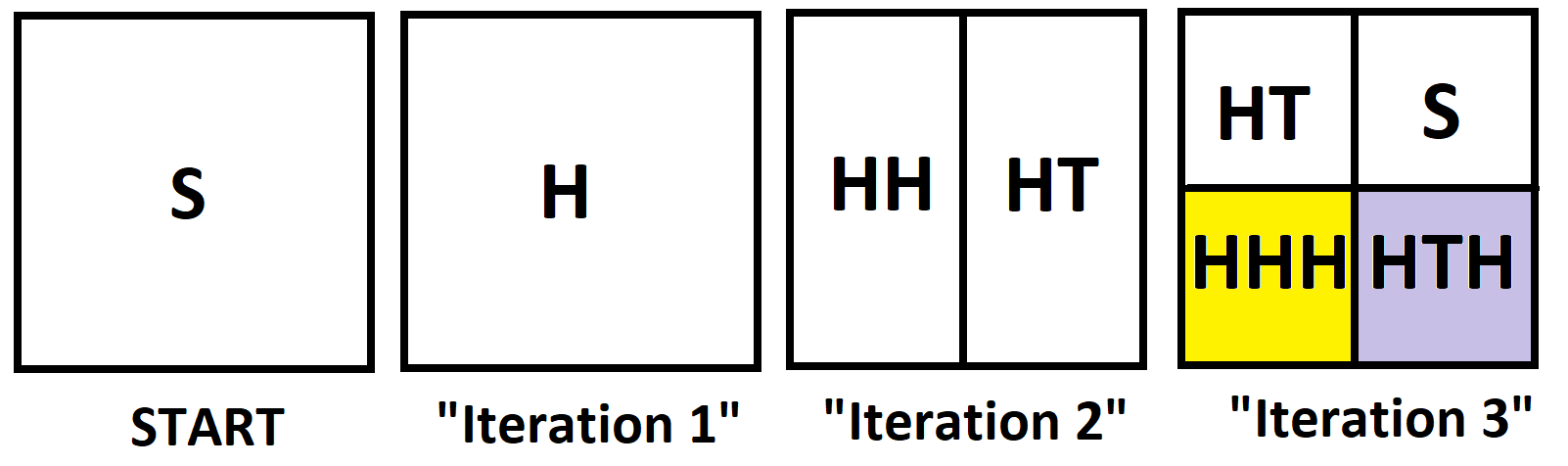
Since we are not keeping track of how many steps fold are taking, we can look at the “HT” cell in the rightmost diagram and say that half these folk HT will end up with HTH, which we don’t want, and half the folk will end up back at start. (Look at the system of garden paths.) Thus we can see we really have the following area model.

And this is the model that arises from this system.

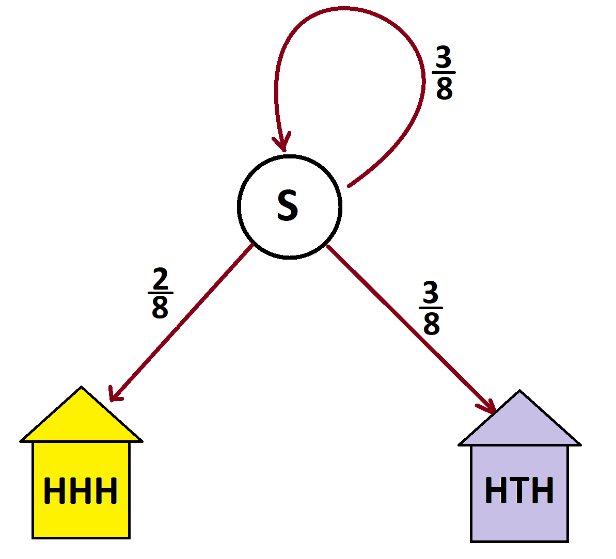
Ignoring the loop back to start, we see that the counts of people that end up in houses HHH and HTH are in a 2:3 ratio. Thus the probability of seeing HHH first is \(\dfrac{2}{5}\) and the probability of seeing HTH first is \(\dfrac{3}{5}\).

 

Practice Problem 3: I will repeatedly toss a coin. What are the chances I will see a head immediately followed by a tail (HT) before seeing two consecutive tails (TT)?

 

REFERENCES

This final section as brought us right up to the point of Arthur Engel’s ground-breaking work on using chip-firing (of which Exploding Dots can be seen to be a special instance). His seminal paper is:

 

Arthur Engel, “The Probabilistic Abacus”, Educational Studies in Mathematics, Vol. 6, No. 1 (Mar., 1975), pp. 1-22.

 

Engel doesn’t explain the mathematical theory of why his chip-firing method works. For that, see J. Laurie Snell’s article “The Engel Algorithm for Absorbing Markov Chains.”

Of course, Dr. James Propp has written a number of lovely essays about Engel’s beautiful work in his Mathematical Enchantment series. See essays 26 and 36, in particular, and also essays 25, 28, and 40.

 

 

 

 

 

Resources