Global Math Project Experiences
3.1 Some U-shaped Graphs
Lesson materials located below the video overview.
One of the first—usually the first—non-straight-line graph one encounters in school is the graph of a quadratic equation. One starts by drawing the graph associated with the quadratic equation to see a beautiful symmetrical U-shaped curve.
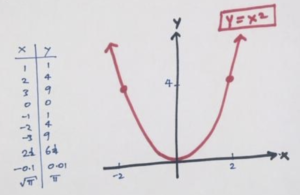
Just to be clear, the graph of an equation is a plot of all the data points that make the given equation a true sentence about numbers. For example, choosing \(x=2\) and \(y=4\) makes \(y=x^2\) a true number sentence, but choosing \(x=3\) and \(y=7\) does not. So we plot the point \(\left(2,4\right)\) as part of the graph of \(y=x^2\), but not the point \(\left(3,7\right)\).
And the graph of \(y=x^2\) is indeed beautifully symmetric. The points \(\left(-2,4\right)\) and \(\left(2,4\right)\) both appear on the graph, as do the points \(\left(-3,9\right)\) and \(\left(3,9\right)\) , and \(\left(-\sqrt{\pi},\pi\right)\) and \(\left(\sqrt{\pi},\pi\right)\) , for instance. We have a U-shaped graph with a vertical line of symmetry.
Practice 1: Is the term “U-shaped” actually correct for the shape of the \(y=x^2\) graph? After all, the sides of the letter U are vertical. Is the graph of \(y=x^2\) ever vertical?
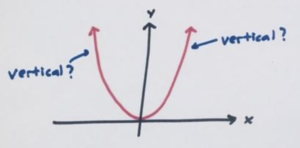
(All solutions to practice questions appear at the end of TEACHER GUIDE to this experience.)
I’ll continue to use the phrase U-shaped curve or U-shaped graph even if it is technically not correct. Let’s simply understand that I am referring to the shape of a quadratic equation graph.
These U-shaped graphs are full of surprises. Here’s one.
Practice 2: Suppose we tilt the graph of \(y=x^2\) (well, rotate it, actually) counterclockwise about the origin just \(0.01\) degrees. Does the \(y\)-axis intercept this tilted graph at some large non-zero value?
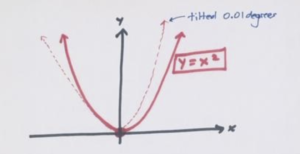
Again, the solutions to all these practice problems appear in the TEACHER GUIDE. But let me help you out with this question right now as it seems extraordinarily tough to answer.
Mathematicians are also human and get scared by questions and math challenges too. But one technique they often employ when faced with a question they don’t first know how to answer is to change the question!
What’s the scariest part of this question? It’s tilting the U-shaped graph. How does one actually do that? I don’t personally know! So, let’s tilt something else instead. What if we keep the graph of the same and tilt the vertical axis \(0.01\) degrees clockwise instead? Does this tilted line intersect the U-shape graph?
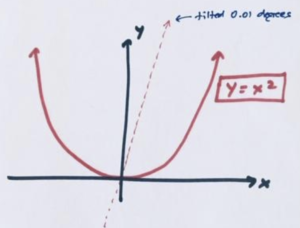
Oh! Hang on! Is this equivalent to answering the original problem?
Here’s the biggest surprise of these U-shaped graphs of all. Many people seem to miss this shocker when they first study quadratic equations.
Practice 3: The graph of \(y=x^2\) is a symmetrical U-shaped curve. The graph of \(y=2x\), on the other hand, is not! It is a straight line through the origin with anti-symmetry if you like—the data plot rises to the right as it decreases to the left.
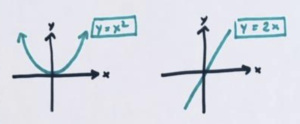
Now for a weird question: What picture would be obtain if we “added” these two graphs?
What could we mean by this?
Let’s look at each \(x\) value and add their matching \(y\) values. For example:
For \(x=1\), we’ll add \((1)^2\) and \(2(1)\) and get \(3\).
For \(x=2\), we’ll add \((2)^2\) and \(2(2)\) and get \(8\).
For \(x=10\), we’ll add \((10)^2\) and \(2(10)\) and get \(120\).
That that is, we are plotting the graph of the equation \(y=x^2+2x\).
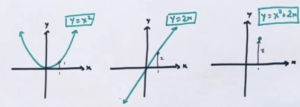
It is clear as that as we put in larger and larger positive \(x\) values, we are getting higher and higher points. The graph rises upwards as we move to the right. (Maybe in a straight line? Maybe in some curved way?)
Things are more interesting to the left for negative \(x\) values: the graph of \(y=x^2\) has data points with positive heights in this region, but the graph of \(y=2x\) has points of negative heights here. We’ll be adding together positive and negative heights. Will they cancel out and give zero heights? Will the positives heights “beat” the negative ones and give an overall graph of positive height? Or will the negative heights “win”?

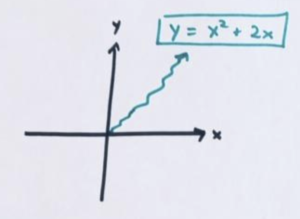
Do plot the graph of \(y=x^2+2x\). Make a table of data values that give true number sentences and plot those data points. Consider enough of them to get a good sense of the shape of the graph. You are in for a surprise!
The surprise is that it is another perfectly symmetrical U-shaped graph just positioned at a different place in the plane. STUNNING and SHOCKING!
In fact, adding together any basic quadratic expression \(y=ax^2\) and a linear expression \(y=bx+c\) is sure to give an expression whose graph is the same symmetrical U-shaped graph, maybe flattened or steepened a bit, and maybe shifted to a new position in the plane.
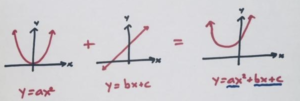
This is just astounding!
That U-shape is astonishingly robust and one cannot help but be transfixed by its robustness.
Of course, one can explain why this graphing phenomenon holds by analyzing the algebra of quadratic equations. But hopefully you were equally shocked by this phenomenon when you first started learning to graph quadratics.
Comment: If you are looking for a review of quadratics, their algebra and their graphs, full of all the surprises and shocks, see www.gdaymath.com/courses.
Now to the issue we’ll explore in these notes.
How ubiquitous are these U-shaped curves from quadratics?
Are the U-shaped curves we see in all sorts of contexts basically the same U-shape, (maybe, as I said, just steepened or flattened a bit and moved or even turned upside-down perhaps)? Are these curves so robust so as to be universal in nature?
For example, school physics tells us that the path of a thrown object follows the arc of a quadratic graph. Is that true? How do we know?

Famous Italian mathematician and physicist Galileo Galilei (1564-1642) wondered about the shape a chain hanging between two poles makes. (We see this shape in hanging power lines, in the shape of ropes that surround sculptures in art museums, and so on.) Is this the same quadratic U-shape? How could we know?

Greek scholars of ancient times used geometry to describe all sorts of special curve. They called one of their curves a parabola and it too is U-shaped.

Algebra wasn’t invented for another 800 years or so and so these scholars did not ask: Is this curve given by a quadratic equation? But we can! So, is it? How could we know?
Is the famous St. Louis Gateway Arch in Missouri of the United States in the shape of a quadratic curve?

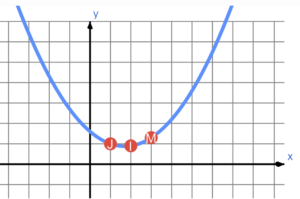
Is the graph of the equation that spells my nickname, JIM, quadratic? This curve passes through the points
\(x=1\), \(y=10\) and the 1st letter of my name is the 10th letter of the alphabet, J;
\(x=2\), \(y=9\) and the 2nd letter of my name is the 9th letter of the alphabet, I;
\(x=3\), \(y=13\) and the 3rd letter of my name is the 13th letter of the alphabet, M.
Let’s answer all these questions—and more! We’re in for a cool adventure!
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


