Recall from lesson 3 we were using the standard leading diagonals that come from the sequences generated by the powers of \(n\).

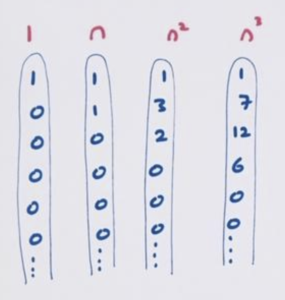
If we trusted seeing rows of constant differences, we could then try to write the leading diagonal of our difference table as a combination of these basic leading diagonals and get a candidate formula for our sequence, which we could then check.

But this set of standard leading diagonals is awkward and hard to work with!

It would be so much easier to work with leading diagonals that look like these.

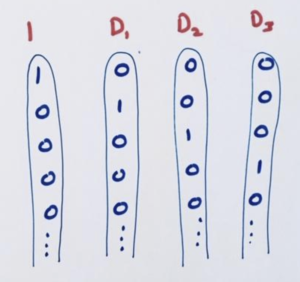
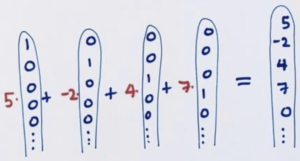
Then we’d know that the diagonal (5 -2 4 7 0 0 0 …), for instance, is given by \(5 \cdot 1-2D_{1}+4D_{2}+7D_{3}\).

We know that the constant sequence of 1s gives us the first leading diagonal. What sequences have \(D_{1}\), \(D_{2}\), \(D_{3}\),and so on, as their leading diagonals?

 

Exercise: Fill in each of these difference tables. Do you recognize any of the sequences?

 

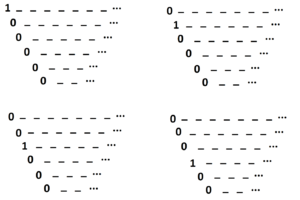
Sir Isaac Newton (1642 – 1727) recognized these sequences as the diagonals of the famous arithmetic triangle, provided one inserts leading zeros into the diagonals.

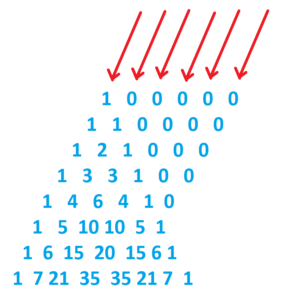
And he knew a formula for the terms of this triangle and hence formulas for these terms of each of these sequences. (See part 3 of www.gdaymath.com/courses/permutations-and-combinations/ .)

 

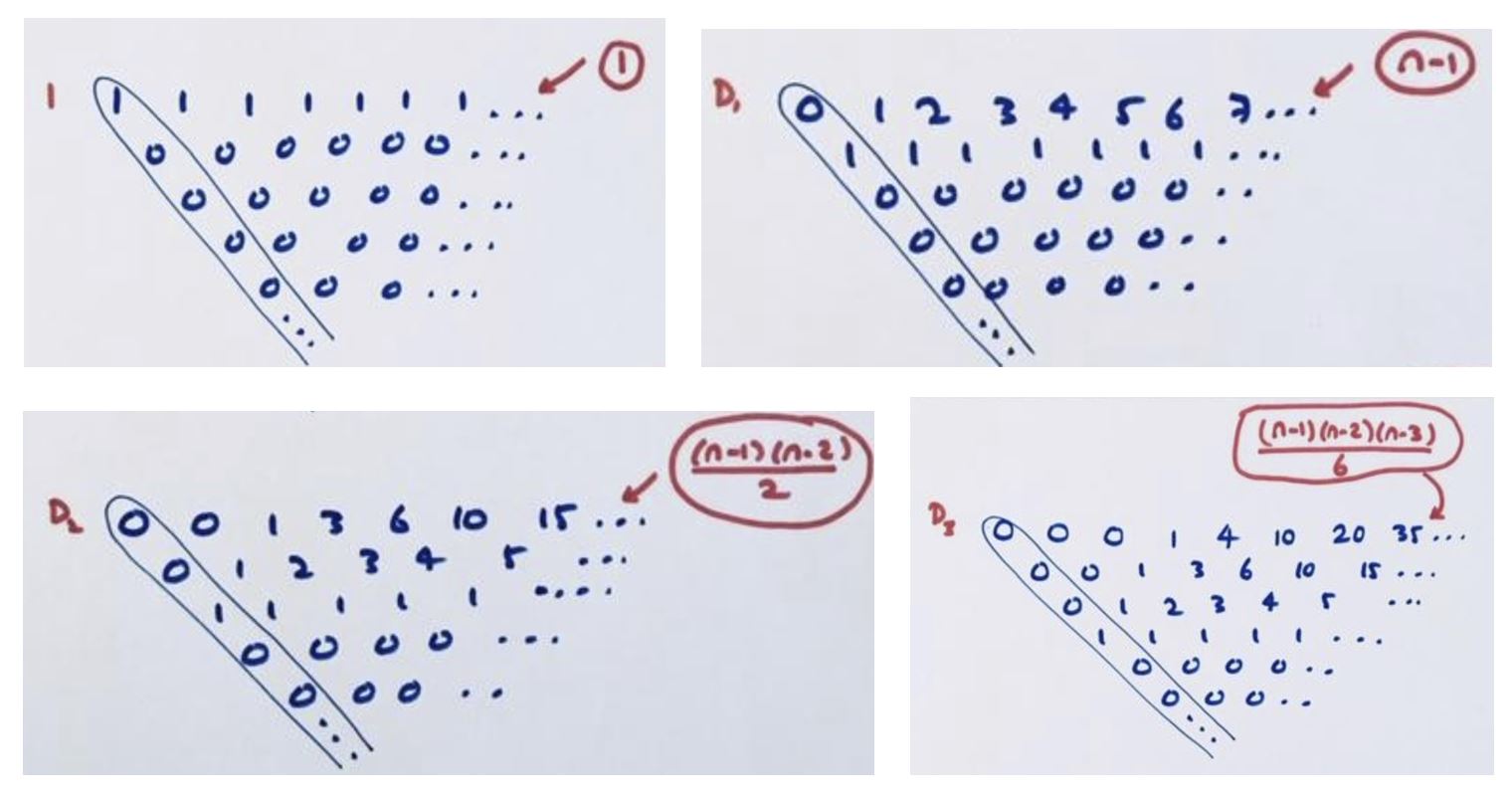
Comment: In general, the sequence that gives the \(k\)th diagonal has terms given by the formula

\(\dfrac{\left(n-1\right)\left(n-2\right)\cdots \left(n-k\right)}{k!}\) .

 

 

Example: Trusting patterns, find a formula for the sequence 3  4  7  12  19  28 ….

 

Answer: We have the following difference table.

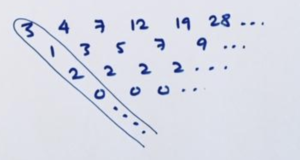
And we readily see its leading diagonal as a combination of our (new) standard diagonals.

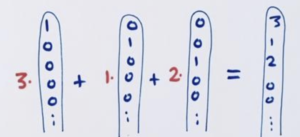
Thus we suspect this sequence is following the formula

\(3 \cdot 1 + 1 \cdot \left(n-1\right) + 2 \cdot \dfrac{\left(n-1\right)\left(n-2\right)}{2}\)

which simplifies to \(n^2-2n+4\). And one check that this formula does indeed work!

 

Practice 1: Trusting patterns, find a formula for the sequence

3   7   29   99   247   503   897   1459   ….

 

Practice 2: Does Newton’s approach give the formula \(n^2\) for the sequence of square numbers 1, 4, 9, 16, 25, 36, …? Does it give the correct formula for the cube numbers?

 

Of course, as we saw, mathematicians never trust patterns. They might be motivated by them, guided by them even, and they might feel the formulas suggested by them should be true, but mathematicians will never be satisfied until they have a logical explanation that ensures patterns really are true.

This next activity illustrates a lovely interplay between patterns and logic.

 

THE SLIDE PUZZLE

This classic puzzle is usually phrased in terms of frogs and toads leap-frogging over each other. Here I’ll just use counters.

Let’s start with two black and two white counters arranged in a row of five boxes as shown.

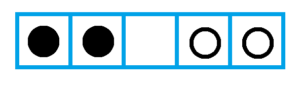
White counters can only move left. Black counters can only move right.

Each move is either a slide (S) in which a counter moves one place over to an empty cell or a jump (J) in which a counter leap-frogs over an adjacent counter (of any color) into an empty cell two places over.

The goal is to have the black and white counters switch positions.

With \(N=2\) counters of each color the puzzle can be solved in 8 moves.

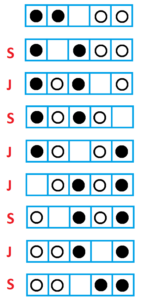
Let \(P\left(N\right)\) be the number of moves required to solve an analogous puzzle with \(N\) black counters and \(N\) white counters arranged in a row of \(2N+1\) boxes. We have shown that \(P\left(2\right)=8\).

a) Find \(P\left(3\right)\) by solving the \(N=3\) version of the puzzle.

b) Find \(P\left(1\right)\), \(P\left(4\right)\), and \(P\left(5\right)\).

c) Assuming we can trust patterns, find a possible formula for \(P\left(N\right)\).

 

Solving the \(N=2\) puzzle followed the pattern of moves

S J S JJ S J S.

Here we have four slides and four jumps.

d) What patterns of moves solves the \(N=1\), \(N=3\), \(N=4\), and \(N=5\) puzzles? How many slides appear in each? How many jumps?

Any conjectures as to how many slides and how many jumps there will be in solving a general puzzle with \(N\) black and \(N\) white counters?   

    

e) With \(N\) black and \(N\) white counters explain why a solution must involve \(N^2\) jumps.  (Use a logical argument this time and don’t rely on patterns.)

f) With \(N\) black and \(N\) white counters how many places to the left must each white counter move and how many  places to the right must each black counter move? Explain why we must have \(P\left(N\right)=2N\left(N+1\right)-N^2\). (Does this match your answer to part c?)

 

g) Solve the puzzle again for the case \(N=3\). This time watch the location of the blank space. Is each of the seven boxes empty at some point of play? Must this be the case?

 

Challenge: Suppose there are \(N\) black counters and \(M\) white counters.

Is it always possible to rearrange the counters so that the black ones sit to the right and the white ones sit to the left? Is there a pattern to the moves required? Is there a general formula for the number of moves required?

 

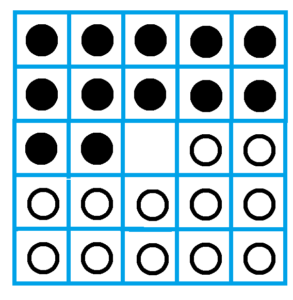
Challenge: Is it possible to interchange the black and white counters in this two-dimensional array? Here counters may move in any direction – left, right, up, down – via slides and jumps.

 

DIFFERENCES THAT REOCCUR

Of course, sequences can exhibit many different types of behavior.

For instance, all the sequences we’ve studied in these notes eventually yield a row of constant values in their difference tables, except one! We saw that the sequence of the powers of two fail to yield a row of constant differences.

So our method will not yield a formula for the powers of two. (But we already happen to know that the \(n\)th power of two is given by \(2^{n}\).

Notice that the leading diagonal for the powers of two is the constant sequence of 1s. It’s actually the sequence of the powers of 1.

 

a) Consider the sequence of the powers of three: 1 3  9  27  81  243  729  …. Show that its leading diagonal seems to be the powers of two.

b) Consider the sequence of the powers of four: 1 4  16  64  256  1024  4096  …. Show that its leading diagonal seems to be the powers of three.

c) Prove that the leading diagonal of the powers of \(a\)

\(1\)  \(a\)  \(a^2\)  \(a^3\)  \(a^4\)  \(a^5\)  \(a^6\)  \(\cdots\)

is sure to be the powers of \(a-1\).

 

Mathematician Robert Jackson noticed that computing the difference table for a leading diagonal that isn’t mostly zeros can lead information about the original sequence.

For example, consider this sequence.

Here’s its difference table.

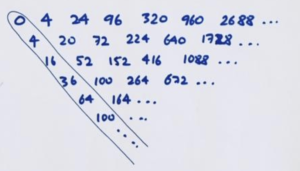
Its leading diagonal doesn’t seem to go to zero. So let’s compute the difference table of this diagonal.

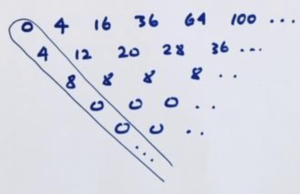
This now is mostly zero.

 

Jackson noticed that this behavior is similar to the behavior of the powers of 2. They too have a leading diagonal that is not going to zero (the powers of 1), but the leading diagonal of that leading diagonal is mostly zero.

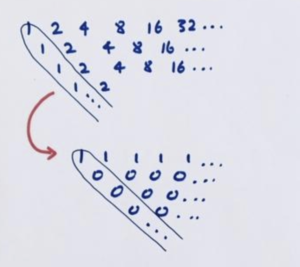
So maybe our original sequence is a “contains” the powers of 2? Let’s try dividing the terms of sequence by respective powers of 2.

\(0 \div 1=0\)

\(4 \div 2=2\)

\(24 \div 4=6\)

\(96 \div 8=12\)

\(320 \div 16 =20\)

\(960 \div 32=30\)

\(2688 \div 64=42\)

\(\vdots\)

Now look at the difference table of this divided sequence.

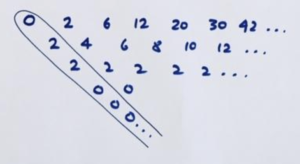
Our methods give the formula \(n^2+n\) for this divided sequence, suggesting that the \(n\)th term of our original sequence must be

\(2^{n}\left(n^2+n\right)\)

and we check that it works!

 

Practice 3: Consider the sequence of numbers

0   9   108   891   5832    32805    166212     780759    …

Draw the difference table for this sequence.

Compute the difference table for its leading diagonal.

Compute the difference table for the leading diagonal of this difference table.

Keep doing this for a while and see that the sequence is exhibiting behavior analogous to that of the powers of three.

Find a formula for the \(n\)th term of this sequence.

 

Of course, not all sequences succumb to the approaches we described thus far. For example, look at the sequence of Fibonacci numbers with each term after the first two is the sum of its previous two terms.

1  1  2  3  5  8  13  21  34  55  89  …

Do our techniques work to give a general formula for the \(n\)th Fibonacci number?

 

The theory of difference methods is still an area of research for mathematicians.

 

Resources