I was recently asked

James: I am required to teach partial fractions to my advanced algebra students. They won’t be taking calculus for another year or more, so the usual motivation for this work–integrating rational functions by partial fractions–is absent. How would you introduce a unit on partial fractions in an algebra class?

Just to be clear: the topic of “partial fractions” is the art of rewriting the reciprocal of a polynomial, such as \(\dfrac{1}{x^2+x-6}\), as a combination of the reciprocals of that polynomial’s factors. For instance

\(\dfrac{1}{x^2+x-6}   = \dfrac{1/5}{x-2}-\dfrac{1/5}{x+3}.\)

Matters are a little more complex if there repeated factors or irreducible quadratic factors. I am not sure the depth to which a school algebra unit on this topic might go.

This challenge intrigued me. I’ve never been required to teach partial fractions in a K-12 setting, and for a while I could not think of a single reason why anyone might by led to and inherently intrigued by the task of rewriting reciprocals of polynomials.

But then it occurred to me that maybe the class class of JUG FILLING puzzles could serve as a compelling segue into partial fractions?

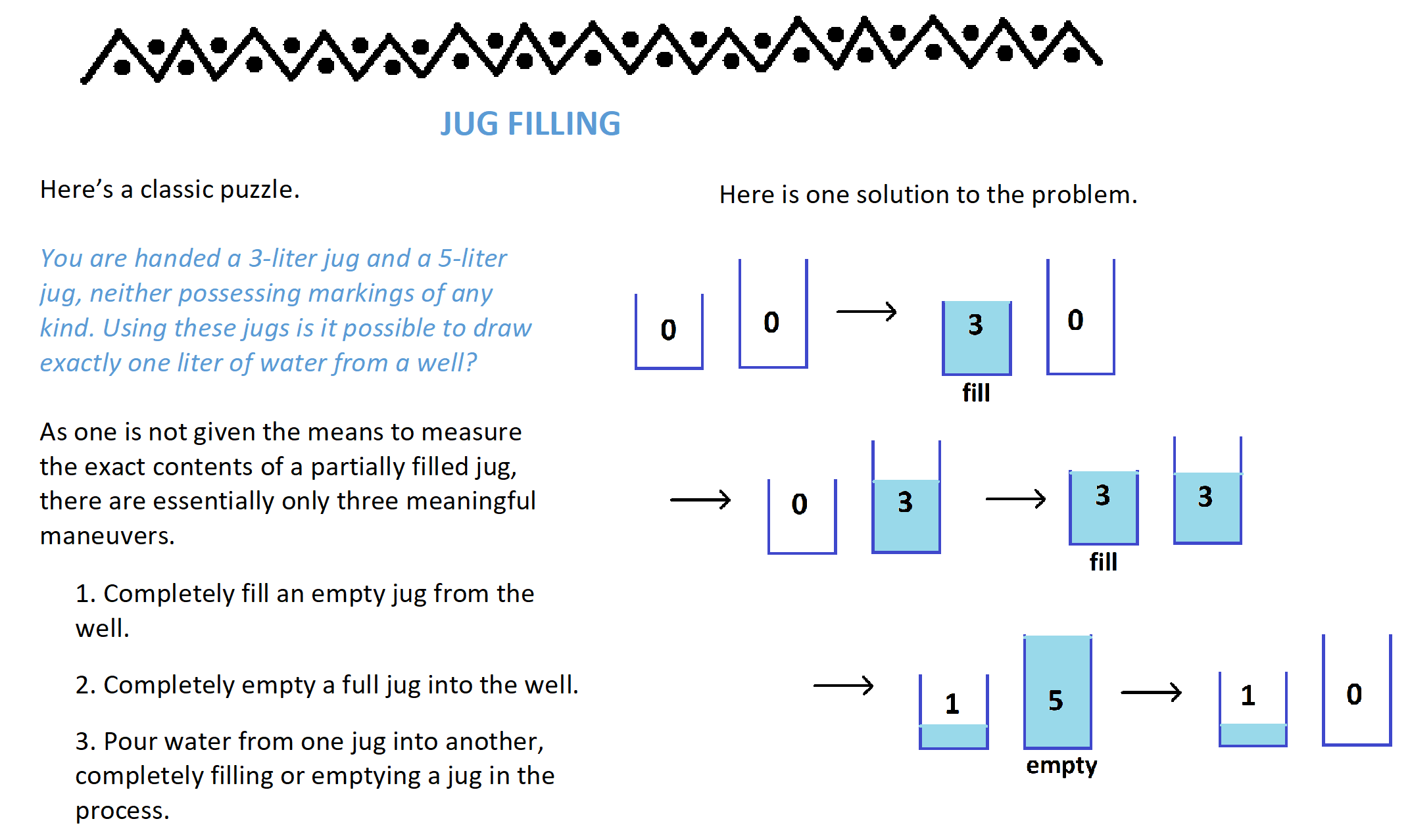
What do you think of the ideas in this document? Partial Fractions

Just the first two pages are relevant to the immediate task at hand (it should be clear how to bounce off of challenge 8 into textbook material). The remaining optional five pages dig deep into the cool number theory behind all this, which, alas, is not part of a typical curriculum.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources