SETTING THE SCENE

Scholars of some 2000 years ago realized that there are certain types of equations that can be readily solved by drawing pictures of squares. And lo, and behold, these became known as equations that can be solved by the “square method.” The Latin word for square is quadrus, and as Latin took on the role of being the official scientific language in the West, these equations became known as the “quadrus equations” or, as we call them today, quadratic equations.

 

Comment: We regularly use the prefix quad in everyday life. It means “four.” A quadrilateral, for instance, is a figure with four sides. A quadruped is an animal with four limbs. Students hold recess in the school quadrangle – a rectangular open area with four right angles.

 

So let’s solve quadrus equations and see the power of area and symmetry in our play. That is, let’s follow the true mathematical story of these equations.

We’ll do this as a series of steps, starting with level 1 equations and building our way up to complex equations in level 6. Each step along the way will exercise our wits and teach us to how think like mathematicians!

 

RESOURCES:

A PDF of these notes appears here: QUADRATICS PD Essay 1.2 (Many people find it easier to read the PDF file rather than this web presentation of the same notes.)

See Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.

 

LEVEL 1 QUADRATICS

Here’s our first level 1 problem.

 

PROBLEM: Solve \(x^2=100\).

 

If you read this out loud—“x squared equals one-hundred”—you notice we say the word square. This problem is asking for the unknown side length of a square whose area is 100.

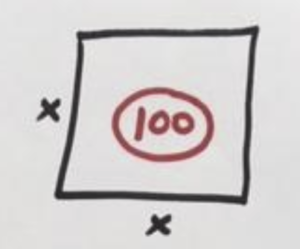
As a geometry problem, there is only one answer, namely \(x=10\). But as we are extending our thinking beyond just literal geometry, we realise there is a second number in arithmetic whose square is also 100, namely, \(x=-10\).

Thus the quadratic equation \(x^2=100\) has two solutions:  \(x=10\) or \(-10\).

 

PROBLEM: Solve \(p^2=49\).

 

This problem is calling the unknown number \(p\) rather than \(x\). Not a problem!

Something squared is \(49\) . That something must be \(7\) or its negative version, \(-7\).   

\(p^2=49\)

\(p=7\) or \(-7\).

 

And this is about it for level 1! Though there can be some slight trickiness.

 

PROBLEM: Solve \(64x^2=25\).

 

It seems compelling to divide both sides of the equation by 64, to that is reads

\(x^2=\dfrac{25}{64}\).

We now see that \(x\) can have a fractional value: \(x=\dfrac{5}{8}\) or \(-\dfrac{5}{8}\).

 

Counting Solutions

It seems that every level one equation we encounter will have 2 solutions: a number and its negative version. But this need not be the case. Consider the equation

\(x^2=0\).   

 There is only one number whose square is zero, namely \(x=0\). So this is an example of a quadratic equation with just one solution.

 

Challenge: Some students might be tempted to write

\(x=0\) or \(-0\)

 not realising that \(-0\) is the same as \(0\). How would you explain to a fellow student that “the opposite of zero is zero”?  

It is possible for a quadratic equation to have no solutions at all! For example, there are no solutions to

\(x^2=-5\).

(Recall from last lesson that positive times positive is positive and also negative times negative is positive. No number multiplied by itself will give a negative answer.)

 

It seems: Each quadratic equation will have either 0, 1, or 2 solutions.

 

We’ll keep checking on the validity of this claim as we progress to more complicated equations.

 

PRACTICE 1: Solve

a) \(2x^2=50\)

b) \(y^2+5=14\)

c) \(100x^2=1\)

d) \(4p^2=0.25\)

e) \(a^2+7=7\)

f) \(x^2=20\)

g) \(x^2=-20\)

 

LEVEL 2 QUADRATICS

Okay. Up a slight notch in difficulty.

 

PROBLEM: Solve \(\left(x+3\right)^{2}=25\).

 

The key here is to “step back” from the problem and see what it is really asking: Something squared is 25. Oh! So the “something” better be \(5\) or \(-5\). And what is the “something”? It is \(x+3\). We have

\(x+3=5\) or \(x+3=-5\)

Subtracting 3 throughout gives

\(x=2\) or \(x=-8\).

Great!

 

PROBLEM: Solve \(\left(2x+4\right)^2=4\).

 

Something squared is 4 and so we have

\(2x+4=2\) or \(-2\)

We want the value of , so let’s subtract 4 throughout

\(2x=-2\) 0r \(-6\)

and dividing through by 2 then gives

\(x=-1\) or \(-3\).

Done!

 

PRACTICE 2: Solve

a) \(\left(4x-6\right)^2=-7\)

b) \(\left(4x-6\right)^2=0\)

c) \(\left(4x-6\right)^2=4\)

d) \(\left(4x-6\right)^2=5\)

 

PRACTICE 3: Solve

a) \(\left(y+1\right)^2-2=23\)

b) \(4\left(p-2\right)^2-16=0\)

c) \(9+\left(34x-77\frac{1}{2}\right)^2=0\)

d) \(\left(x-\sqrt{2}\right)^2=5\)

 

LEVEL 3 QUADRATICS

Let’s now go up another level. When one sees a level 3 problem for the very first time it is SHOCKING! It looks completely different from those in levels 1 and 2.

 

PROBLEM: Solve \(x^2+6x+9=25\).

 

This is an opportunity to exercise two key steps in solving a problem.

 

STEP 1: Be your honest human self and acknowledge your human reaction to the problem!

 

If a problem looks scary, go GULP! and say “This problem looks scary.” If it looks cool and fun say “This looks fun.” If it looks confusing and you don’t know what to do say “I don’t know what to do!”

Mathematics is a human enterprise, made by humans, for humans, so be your honest human self.

Next, take a deep breath and

 

STEP 2: DO SOMETHING! Anything!

 

If you need to take a break to let your brain mull on the problem, take a quick break. Or maybe you can underline some words in the question, or draw a diagram, or read the question backwards. Just do something! You will be surprised how powerful taking a first piece of action—of any kind!—can be in getting going on a problem.

 

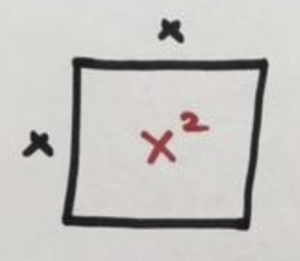
So what about our current problem, solving \(x^2+6x+9=25\)?

 

If I read it out loud, I do hear the word “square” again. I could, at least, draw a picture of a square to match the \(x^2\) term. That’s something!

But there is also a \(6x\) term. Could I add that to the picture? Sure, I can see how to add an area of \(6x\).

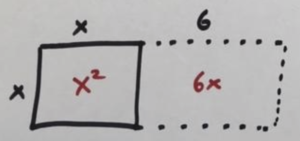
But here I am drawing a picture of an unsymmetrical rectangle. And remember, from the last lesson we learned that symmetry is our friend. So can we add an area of \(6x\) to our picture in a symmetrical way? Sure! Let’s split that area and add on two three-by-\(x\) regions as shown.

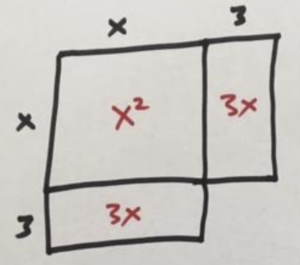
Now we see we have a picture of an incomplete square. It feels absolutely compelling to complete the picture of the square! The final corner is a 3-by-3 square of area 9. And this is the precisely the number problem wants!

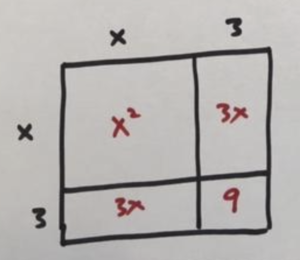
So our picture of areas \(x^2\) and \(6x\) and \(9\) is precisely the picture of an \(x+3\) by \(x+3\) square.

Now the original problem wants \(x^2+6x+9\) to equal \(25\). So we want the area of our square to be \(25\). That is, we see we need to solve

\(\left(x+3\right)^2=25\)

and that is a level 2 problem we’ve already solved!   We have

\(x+3=5\) or \(-5\)

\(x=2\) or \(-8\).

And one can double check that both \(x=2\) and \(x=-8\) really do make \(x^2+6x+9\) equal to \(25\).

 

So this is the challenge of level 3:

Recognise complicated-looking expressions as level 2 problems in disguise.

It’s fun!

 

PROBLEM: Solve \(x^2-8x+16=17\).

 

Okay, we have an \(x^2\) term, so let’s draw a square. In fact, since we know we are going to add on to this picture to make an even larger square, let’s just go ahead and draw a big square divided into four symmetrical pieces right away.

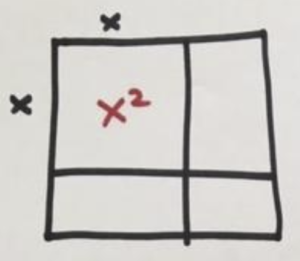
We need to include an “area” of \(-8x\). (Remember, we are pushing our diagrams beyond geometry to speak general truth about all arithmetic.) We do it in a symmetrical way.

We must have side lengths of \(-4\) in the picture.

 

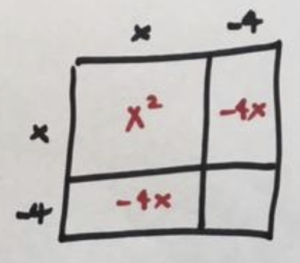
And so the area of the final piece of the completed square is \((-4)\times (-4)=16\), which is precisely the value the problem wanted.

Thus we see that \(x^2-8x+16\) is really an \(x-4\) by \(x-4\) square. We actually being asked to solve

\(\left(x-4\right)^2=17\).

Now the number 17 is awkward, it doesn’t have a nice square root. (Since \(\sqrt{16}=4\) we have that \(\sqrt{17}\) will be a number a little over four.)  Be we can write our answers in terms of the square root of 17 and its negative version.

\(x-4=\sqrt{17}\) or \(-\sqrt{17}\).

Adding four gives

\(x=\sqrt{17}+4\) or \(-\sqrt{17}+4\).

 

Comment: Some people are fussy and prefer to write numbers like this with the integers mentioned first and the roots second. So some might present these answers as

\(x=4+\sqrt{17}\) or \(4-\sqrt{17}\).

Mathematics does not care, but your curriculum might!

PRACTICE 4: Solve

a) \(p^2-6p+9=9\)

b) \(x^2-4x+4=1\)

c) \(x^2-20x+100=7\)

d) \(r^2-16r+64=-2\)

e) \(x^2+2\sqrt{5}x+5=36\)

f) \(x^2-2\sqrt{2}x+2=19\)

 

PRACTICE 5: Solve for \(x\) giving your answer in terms of  \(A\) and \(B\).

\(x^2+2Ax+A^2=B^2\)

 

 

 

SOLUTIONS

 

 

Resources