SETTING THE SCENE

We’re feeling good about our square method. By completing the picture of a square—literally!—we can solve some complicated quadratic equations. In fact, let’s keep going and show how this square method solves all quadratic equations.

 

Just to be clear, any expression of the form \(ax^2+bx+c\) is called a quadratic expression and a quadratic equation is any equation that can be written in the form \(ax^2+bx+c=d\).

 

RESOURCES:

A PDF of these notes appears here: QUADRATICS PD Essay 1.3.   (Many people find it easier to read the PDF file rather than this web presentation of the same notes.)

See Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.

LEVEL 4 QUADRATICS

Consider this problem.

 

PROBLEM: Solve \(x^2-4x+3=15\).

 

This looks just like a level 3 problem. Is there some hidden difficulty? Let’s find out!

 

Start by drawing the square. We have an \(x^2\) piece and two pieces of “area” \(-2x\). Thus we have two side lengths of \(-2\).

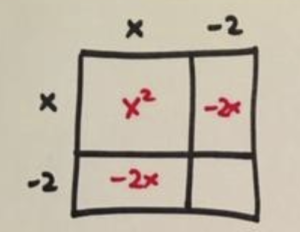
Completing the picture of the square we see we have a final piece of area \(4\).

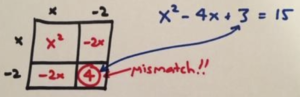
And that’s the difficulty! The square wants the number \(4\) but the problem has only the number \(3\). Oh dear!

 

What can we do?

 

PRINCIPLE: If there is something you want in math, just make it happen! (And deal with the consequences.)

 

Can we turn that “3” into a “4”?

Sure. Let’s just add 1 to it! But there are consequences. If we add 1 to the left side of an equation, we must do the same to the right side as well.

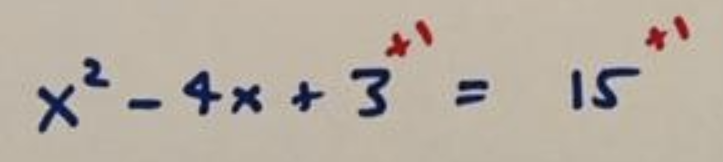
Now we have the equation \(x^2-4x+4=16\) with the left side perfectly matching the pieces of the \(x-2\) by \(x-2\) square. So this is really the equation

\(\left(x-2\right)^2=16\),

which is a level 2 problem!

\(x-2=4\) or \(-4\)

\(x=6\) or \(-2\)

Fabulous!

 

PROBLEM: Solve \(x^2+10x+30=69\).

 

Let’s draw the square. We have an \(x^2\) piece and two \(5x\) pieces. Thus we have two side lengths of \(5\) meaning we want a final piece of area \(25\).

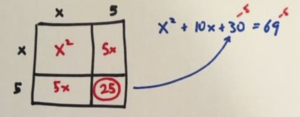
But we don’t have “25” in the problem: instead it’s 30. So let’s subtract 5 and work with the equation \(x^2+10x+25=25\) instead.

 

And why do we like \(x^2+10x+25\)? Because it is an \(x+5\) by \(x+5\) square. So, the problem we really wish to solve is

\(\left(x+5\right)^2=64\).

And this is a level two problem.

\(x+5=8\) or \(-8\)

\(x=3\) or \(-13\)

 

Isn’t this just grand?

 

PRACTICE 1: Solve

a) \(f^2+8f+15=80\)

b) \(w^2+90=22w-31\)

c) \(x^2-6x=3\)

 

LEVEL 5 QUADRATICS

We’re ready for more!

 

PROBLEM: Solve \(x^2+3x+1=5\).

 

Let’s go ahead and use the square method.

But we soon see that we are dealing with awkward fractions! They are not fun.

 

PRACTICE 2 (OPTIONAL): Push on with this problem and do work with fractions. Show that the square method eventually gives the solutions \(x=1\) or \(x=-4\). (The square method will never let you down!)

 

But is there a way we can avoid awkward fractions? That’s is, can we be mathematicians and work to avoid hard work?

The problem lies with the middle coefficient, the number “3.” It is odd, and so does not split into two nicely.

Is there a clever way then we can make that middle number even?

 

IDEA 1: Add \(x\) to both sides of the equation.

 

Let’s solve instead

\(x^2+4x+1=5+x\).

 

But then we’ll have an answer for \(x\) that still involves \(x\) on the right, and so wouldn’t be an actual number answer in the end. Hmmm.

 

IDEA 2: Double everything.

 

Why not solve instead \(2x^2+62=10\)?

We now have an even number in the middle.

 

Let’s draw the square.

But then we see we have a problem: the piece of area \(2x^2\).

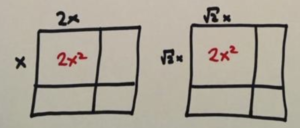
We could think of this piece as \(x\) times \(2x\), but then we are ruining our symmetry. (Remember, symmetry is our friend. We want to keep things square and not make rectangles.)

 

To keep it square could use \(\sqrt{2}x\)  times \(\sqrt{2}x\). But if we didn’t want to work with fractions, we probably don’t want to with square roots either!

 

PRACTICE 3 (OPTIONAL): Push on with this problem and do work with the square roots. Show that the square method again eventually gives the solutions \(x=1\) or \(x=-4\).

 

So, what can we do? Both our ideas were good. They just turned out not to be helpful.

 

Comment: This the process of doing real mathematics! One often has brilliant ideas that, well, turn out not to be helpful. The thing to do then is to mull and think and wait for a next brilliant idea that just might work. This might take minutes, hours, days, even months or years for a particularly tough problem!

 

After some mulling and thinking it might occur to you to try the following.

 

IDEA 3: Instead of doubling everything, try multiplying everything by four!

 

This then gives us the equation

\(4x^2+12x+4=20\),

and this is lovely. The first term, \(4x^2\), is a nice perfect square and the middle number is even.

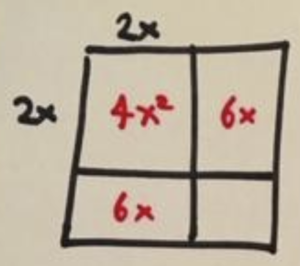
Something times \(2x\) makes \(6x\), so we must have side lengths of \(3\), and the final piece of the area is \(9\).

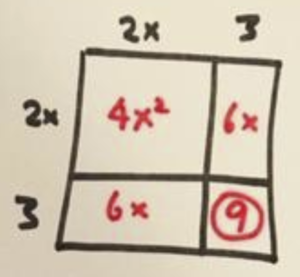
Adding \(5\) to both sides gives us the equation

\(4x^2+12x+9=25\)

and the left side of this equation is precisely the \(2x+3\) by  \(2x+3\) square. We are solving

\(\left(2x+3\right)^2=25\)

which is back to being a level two problem!

\(2x+3=5\) or \(-5\)

\(2x=2\) or \(-8\)

\(x=1\) or \(-4\)

Wow!

 

Multiplying through by 4 unlocked the problem!

 

PROBLEM: Solve \(x^2+7x-2=5\).

 

We have an odd middle term. If we choose to avoid fractions we can multiply through by 4 and solve instead \(4x^2+28x-8=20\).

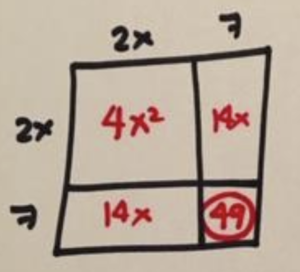
The square method shows we really want the number \(49\), not \(-8\). So let’s add \(57\) to each side and work with

\(4x^2+28x+49=77\).

The number on the right is awkward. Oh well!

We have

\(\left(2x+7\right)^2=77\)

\(2x+7=\sqrt{77}\) or \(-\sqrt{77}\)

\(2x=\sqrt{77}-7\) or \(-\sqrt{77}-7\)

\(x=\dfrac{\sqrt{77}-7}{2}\) or \(\dfrac{-\sqrt{77}-7}{2}\).

 

PRACTICE 4: Solve as many of these as you feel like doing.

 a) \(w^2-5w+6=2\)

b) \(x^2+9x+1=11\)

c) \(p^2+p+1=0.75\)

d) \(x^2=10-3x\)

e) \(x^2-x-1=2\frac{3}{4}\)

f) \(x^2+3=9\)

 

LEVEL 6 QUADRATICS

This is it: the final level!

Here’s a next problem that has every possible difficulty that can ever occur when solving a quadratic equation.

 

PROBLEM: Solve \(3x^2+5x+1=9\).

 

The first issue is that we now have a number in front of the \(x^2\) term. All other levels avoided this.

But in level four we did introduce a factor of four into our equations to work with \(4x^2\), which we saw was a nice perfect square: it is \(2x\) times \(2x\).

Here we have \(3x^2\), which is not a nice perfect square. Can we make it one?

Yes! Let’s multiply the equation through by 3 and work with

\(9x^2+15x+3=27\).

Great! The first term is , a nice square.

But we have an odd middle number, that 15! So, let’s multiply through by 4 to fix that.

 

A WORRY! Will doing so ruin our perfect square at the front?

 

We get

\(36x^2+60x+12=108\).

Phew!  is still a nice perfect square. In fact, multiplying a perfect square by 4 will never “ruin” a perfect square. (Can you see why?)

 

So now things look good for the square method.

We see the square wants the number 25, so let’s add 13 to both sides and work with

\(36x^2+60x+25=121\).

 

And why did we do all this crazy work? To recognize \(36x^2+60x+25\) as a square: it is a \(6x+5\) by \(6x+5\) square. We have a level 2 problem!

\(\left(6x+5\right)^2=121\)

\(6x+5=11\) or \(-11\)

\(6x=6\) or \(-16\)

\(x=1\) or \(-\frac{8}{3}\)

 

PROBLEM: Solve \(5x^2-3x+2=4\).

 

Let’s multiply through by 5 to make a perfect square up front.

\(25x^2-15x+10=20\)

 

Now let’s multiply through by 4 to make the middle term even.

\(100x^2-60x+40=80\)

 

The square method shows we want the number \(49\). Let’s subtract 31 from each side.

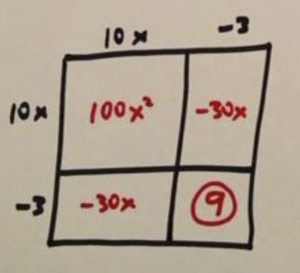
\(100x^2-60x+9=49\)

\(\left(10x-3\right)^2=49\)

\(10x-3=7\) or \(-7\)

\(10x=10\) or \(-4\)

\(x=1\) or \(-0.4\)

 

PRACTICE 5: Solve as many of these you feel like doing.

a) \(2x^2=9\)

b) \(4-3x^2=2-x\)

c) \(\alpha^2-\alpha+1=\frac{7}{4}\)

d) \(3x^2+3x+1=19\)

e) \(-3x^2+3x+1=19\)

f) \(10k^2=1+10k\)

 

PRACTICE 6: Consider \(4x^2+6x+3=1\). Does it look like this quadratic equation will have problems when solving it? Does it have problems as you try to solve it? What can you do to obviate the difficulties you encounter?

 

 

EVERYTHING IS LEVEL 2!

We have illustrated that every quadratic equation \(ax^2+bx+c=d\) is really just a level 2 question in disguise.

 

\(\left(something\right)^2=number\)

 

And as we noted in the last lesson, each such equation has either 0, 1, or 2 solutions. As such:

Any quadratic equation \(ax^2+bx+c=d\) has either 0, 1, or 2 solutions.

 

PRACTICE 7:

a) Design a quadratic equation that has two negative solutions.

b) Design a quadratic equation with just one solution, namely, \(x=4\).

c) Design a quadratic equation with \(x=2\) and \(x=10\) as solutions.

 

LOTS OF ADDITIONAL PRACTICE

 

PRACTICE 8:

a) A rectangle is twice as long as it is wide. Its area is 30 square meters. What are the dimensions of the rectangle?

b) A rectangle has one side 4 meters longer than the other. Its area is 30 square meters. What are the dimensions of the rectangle?

 

PRACTICE 9:

a) Solve \(\tau^2-5\tau+7=1\).

 

The symbol \(\sqrt{}\) means the positive root of a number. (For instance, \(\sqrt{9}=3\), and not \(-3\), even though there are two numbers whose squares are \(9\).)  This is a mathematics convention, and it can be confusing as it is ignoring symmetry.

But we can say that if \(x\) is a positive number, then we have \(x=\left(\sqrt{x}\right)^2\).

 

b) Solve \(x-5\sqrt{x}+7=1\).

HINT: Look at part a).

 

c) Solve \(x-2\sqrt{x}=-1\).

 

d) Solve \(x+2\sqrt{x}=5=10\) and be clear why this equation has only one solution!

 

e) Solve \(2u^4+8u^2+7.5=0\).

 

PRACTICE 10: Consider \(y=2\left(x-4\right)^2+6\). What value for \(x\) produces the smallest possible value for \(y\)? Why?  

 

PRACTICE 11: Find one solution to \(\left(x+1\right)^3=27\).

 

PRACTICE 12 (TOUGH!): In the following equation, solve for \(x\) in terms of \(a\) and \(b\).

 \(x^2-\left(a+b\right)x+ab=0\).

HINT 1: Multiply through by 4 just in case \(a+b\) is odd.

HINT 2: \(\left(a+b\right)^2-4ab\) equals \(a^2-2ab+b^2\), which happens to equal \(\left(a-b\right)^2\). (Check these claims.)

 

PRACTICE 13 (OPTIONAL): This problem will require you to multiplying through by 4 many times!

a) Solve \(x^2+x=2\).

b) Solve \(2x^2+x=3\).

c) Solve \(4x^2+x=5\).

d) Solve \(8x^2+x=9\).

e) Solve \(16x^2+x=17\).

If you are game …

f) Find the solutions to \(2^{N}x^2+x=2^{N}+1\).

 

 

SOLUTIONS

 

 

Resources