SETTING THE SCENE

Recall the practice of the Factor Theorem.

PROBLEM: Consider the quadratic expression \(x^2+3x-10\).

a) Show that putting in \(x=2\)makes this expression zero.

b) Show that \(x-2\) is a factor of \(x^2+3x-10\).

Answer: a) We have \((2)^2+3(2)-10=0\), as hoped.

b) By the Factor Theorem, it must be the case then that \(x-2\) is a factor of the quadratic expression.

If we wish to actually find the other factor, we can draw an unsymmetrical rectangle with the information we have and deduce its other side length to be \(x+5\).

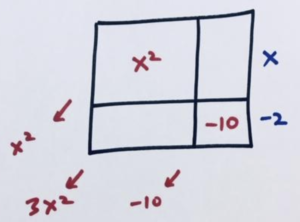
Or we can perform our sneaky algebra.

\(x^2+3x-10=x\left(x-2\right)+2x+3x-10\)

\(=x\left(x-2\right)+5x-10\)

\(=x\left(x-2\right)+5\left(x-2\right)+10-10\)

\(=x\left(x-2\right)+5\left(x-2\right)\)

We see \(x^2+3x-10=\left(x+5\right)\left(x-2\right)\).

Let’s now apply the Factor Theorem to deduce classic mathematics formulas.

READ MORE HERE: QUADRATICS PD Essay 4.3

(See too Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources