SETTING THE SCENE

We ended the last essay on a big note:

The graph of any quadratic equation \(y=ax^2+bx+c\) is sure to be a symmetric U-shaped curve, situated somewhere in the plane.

And the important word here is symmetry. As we full well know, once we have symmetry in a scenario, we have a good friend at our aid!

In this lecture, we’ll show how the simple power of symmetry makes the graphing of quadratic equations beautifully natural and stunningly straightforward!

But first, here is something curious.

My full names is James Stuart Tanton and my initials thus are JST. So consider this quadratic equation:

\(y=-4x^2+21x+7\).

Put in the values 1, 2, and 3 in turn and out come the values:

\(-4\cdot 1^2+21 \cdot 1-7=10\)

\(-4\cdot 2^2+21 \cdot 4-7=19\)

\(-4\cdot 3^2+21 \cdot 3-7=20\).

And notice: The 10^th letter of the alphabet is J, the 19^th letter of the alphabet is S; the 20^th letter of the alphabet is T. This quadratic spells out my initials!

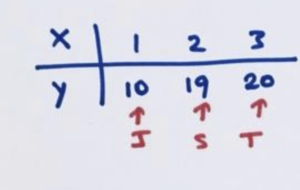
Many people like to call me JIM. So consider …

READ MORE HERE: QUADRATICS PD Essay 6.1

(See too Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources