Quadratics
6.2 The Full Power of Symmetry
Lesson materials located below the video overview.
SETTING THE SCENE
Through the power of symmetry we’ve started graphing quadratic equations with ease. We noticed, for instance, that for
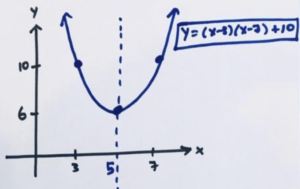
\(y=\left(x-3\right)\left(x-7\right)+10\)
the \(x\) values \(3\) and \(7\) are interesting and led us to two symmetric points on the symmetric curve. Then common sense allowed us to swiftly sketch the equation’s graph.
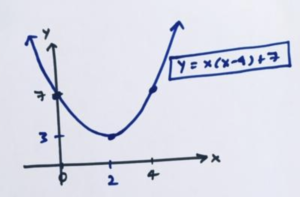
And for \(y=x\left(x-4\right)+7\) the values \(0\) and \(4\) are interesting.
But most quadratic equations are presented in a different, namely, in the form
\(y=ax^2+bx+c\).
Is there a way to identify interesting values in such equations?
READ MORE HERE: QUADRATICS PD Essay 6.2
(See too Edfinity.com/XXX for a robust source of curriculum practice problems for you collate, organise, and use.)
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


