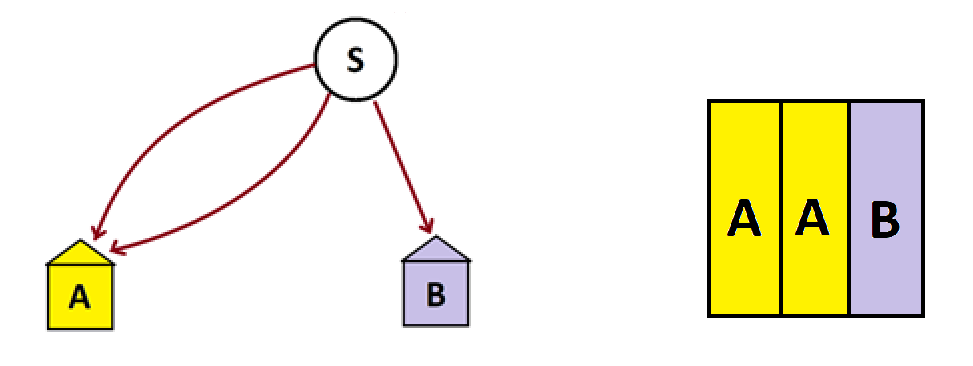
Consider again the infinite garden path system of lesson 2.3.

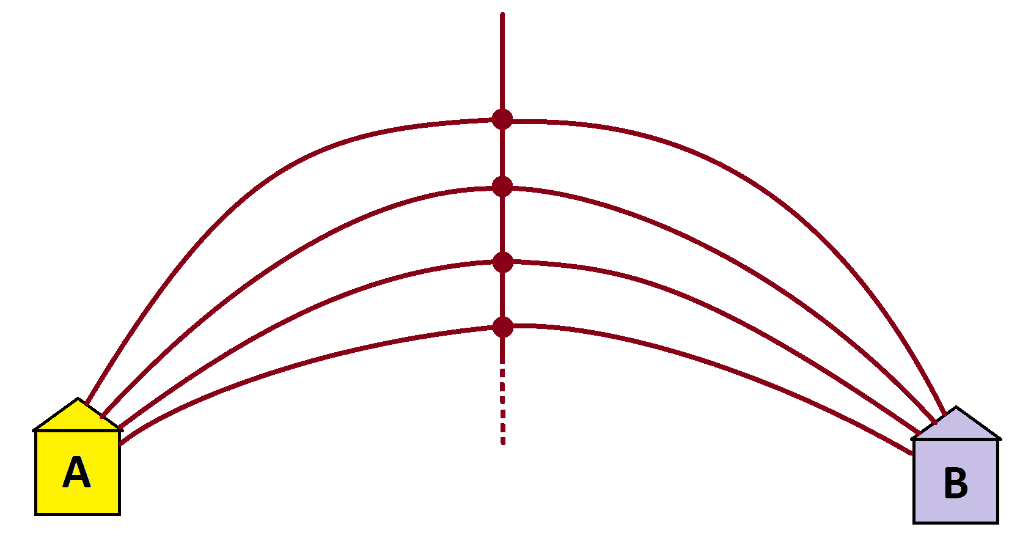
Folk heading down this system first encounter a three-way fork. Those who turn to the left head to house A, those who turn to the right head to house B, and those who go straight repeat this process with another three-way fork. This garden system has infinitely many forks (we are certainly playing a game of the mind here—we humans will never be able to build such a system) and we have to assume that an infinite number of people will be walking through this system.

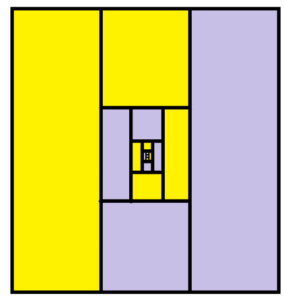
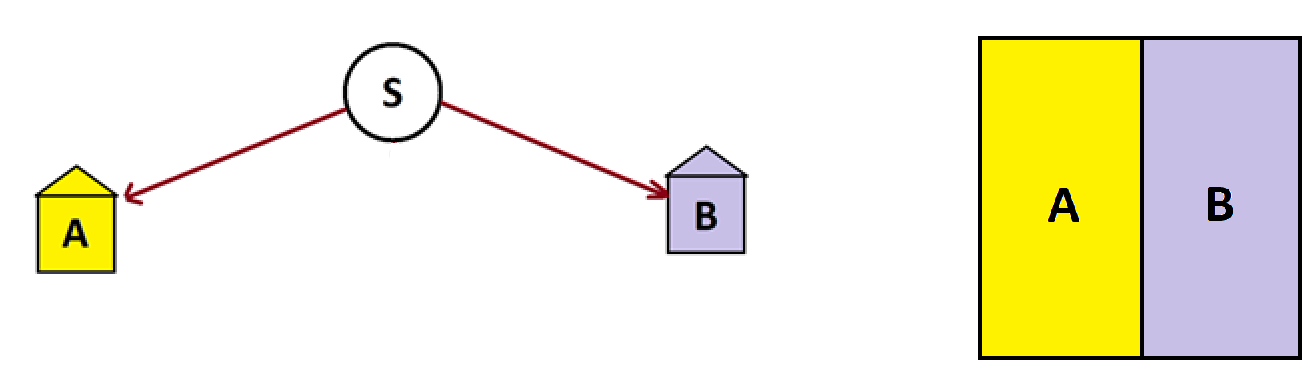
In lesson 2.3 we were led to the following area-model diagram showing, at the end of time, half the people sent through this system will end up in house A and half will end up in house B.

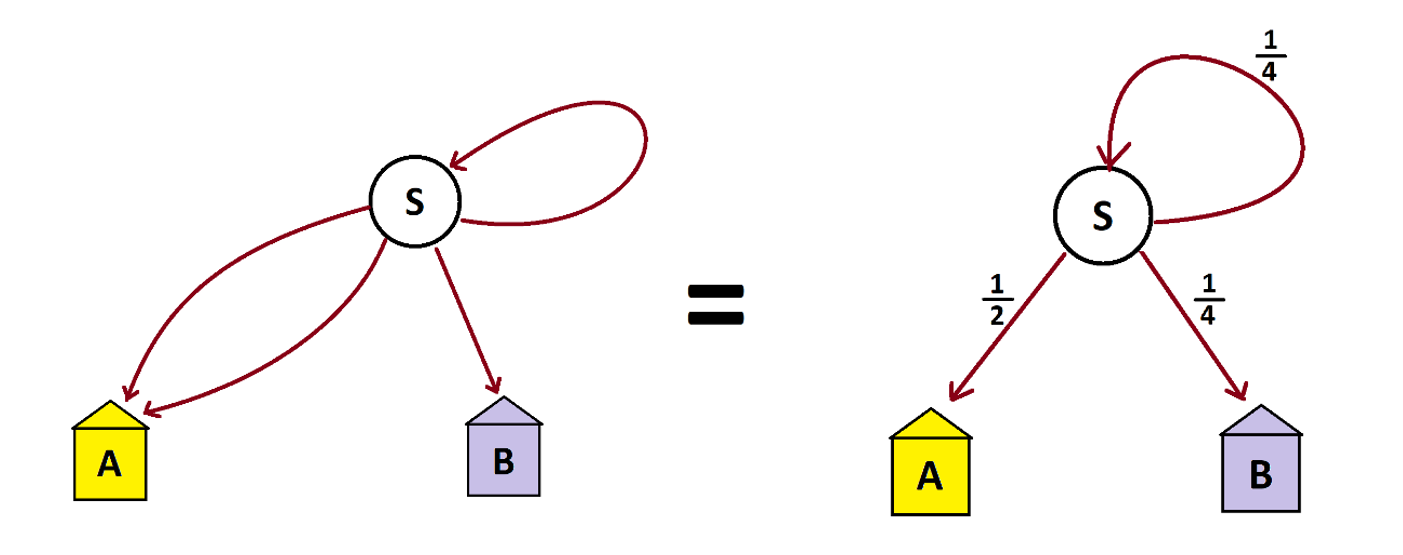
Notice that any subset of people who head straight at a fork are sent to an identical fork with the same infinite structure below it. It is as though we sent these people back to start.

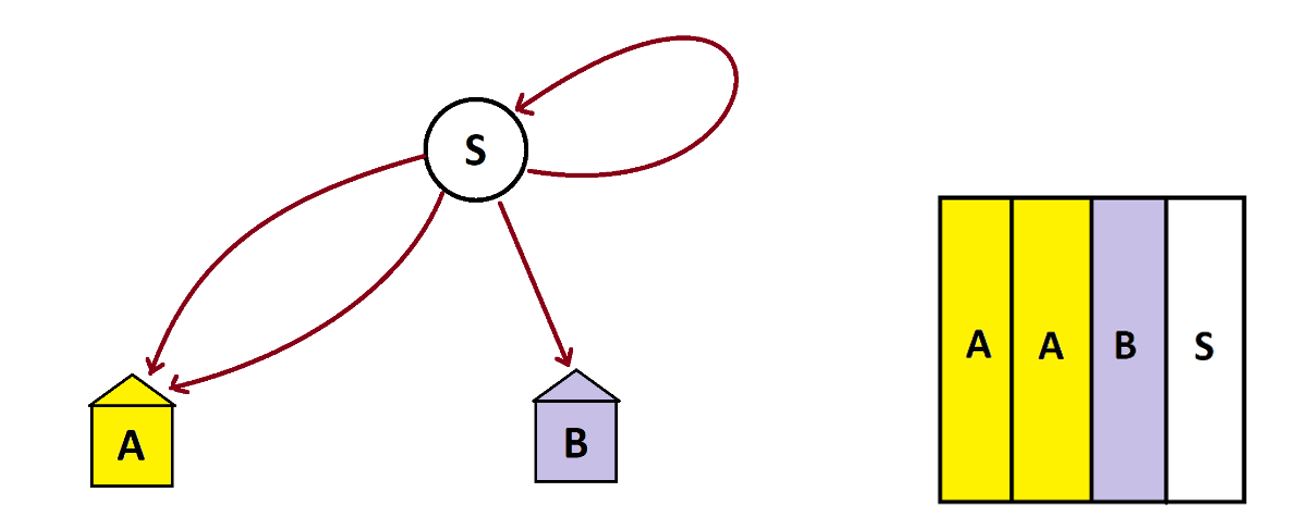
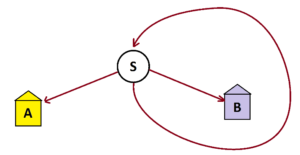
This means we can simplify our garden-path diagram by doing exactly that! Let’s designate a starting location for people, label it S, and draw a single three-way fork at that start location, with people turning to the left heading to house A, people heading to the right to house B, and the people going straight returning to start to repeat the entire process.

 

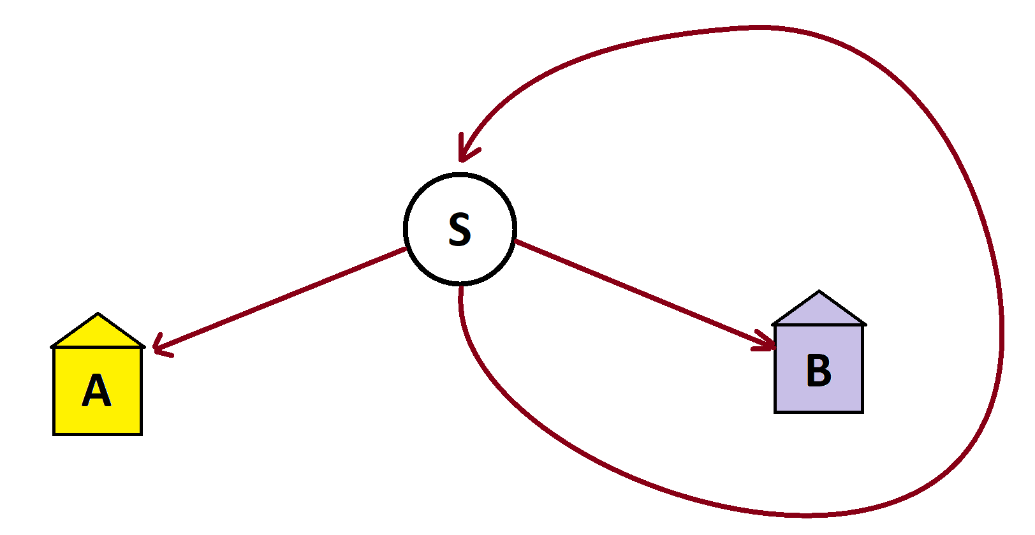
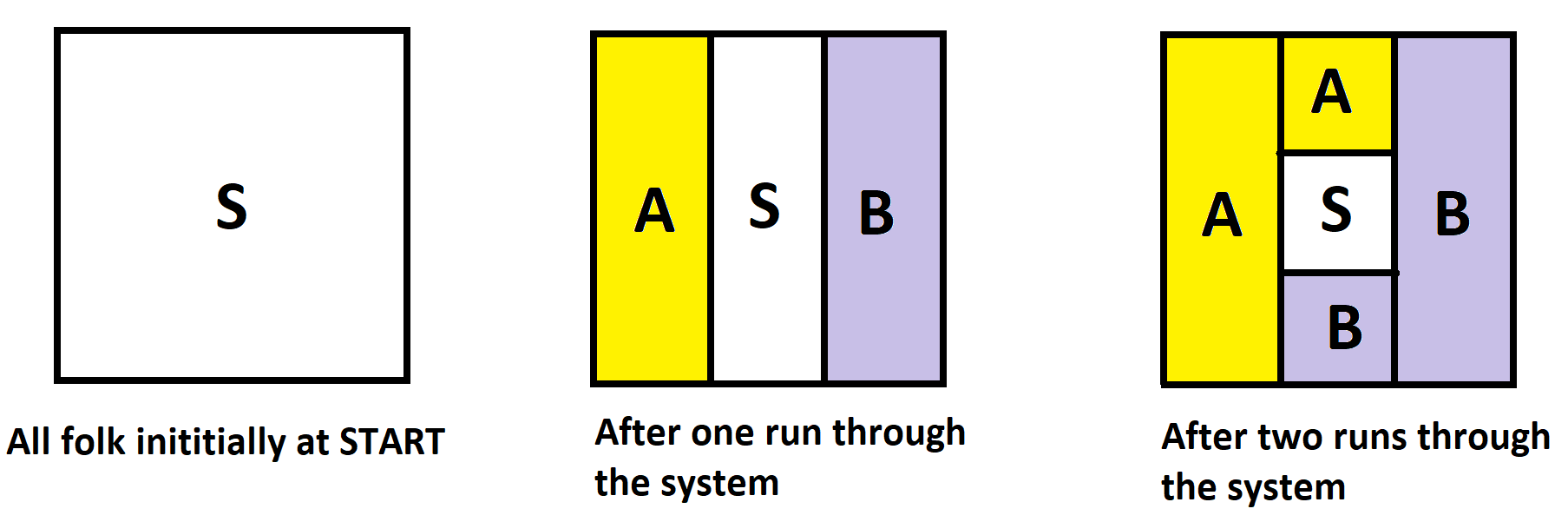
Initially we have an inconceivably large number of people in the start node S. After one run through the system, one third of those folk end up in house A, one third end up in house B, and one third end up back at start.

After a next run through the system, those at start split into thirds again. And after another run through the system, those at start yet again split into thirds again. And so on.

We see that we are generating the same infinite spiral picture above and coming to the same conclusion that, at the end of time, half the people in the system will end up at house A and half in house B.

 

But we could also argue that, eventually, each and every person will end up in a house—either house A or house B. Some people might end up there right away. Others might go back to start a few times and then end up in a house. Others might go back to start tens of thousands of times before heading into a house. Since we do not care how many times people go back to start before entering a house, we could argue that our infinite system is philosophically equivalent to a system with everyone entering a house right away.

We conclude again that half the people will end up in house A and half will end up in house B.

 

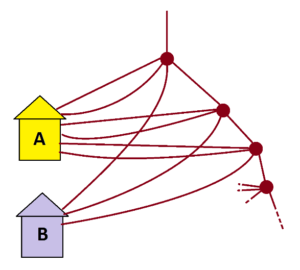
Let’s double-check this reasoning by examining a more complicated system. Consider this example.

This corresponds to garden path system with an infinite number of four-way forks, each with two paths leading to house A, one path leading to house B, and one path leading to an identical four-way fork.

Divide a square into quarters this different way and see a pretty design emerge.

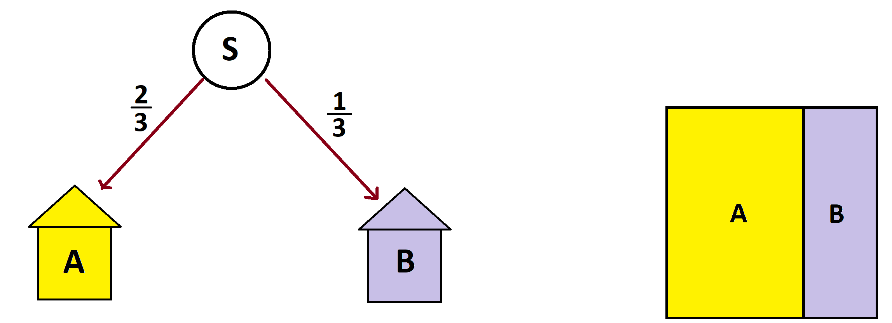
And we see that two-thirds of the people end up in house A and one-third in house B.

But we could have seen this by arguing that, philosophically, this garden path system is equivalent to one without a loop back to start: after all, everyone from start will eventually follow a path to a house.

The two-thirds and one-third distribution is clear.

 

Comment: We could have presented this example as a weighted garden path system.

Notice that double the number of people head to house A than they do to house B. So when we ignore the loop back to start for philosophical reasons, we need to keep in mind that 2:1 ratio. It must be that two-thirds of people go to house A and one-third to house B.

 

 

A Complicated Example:

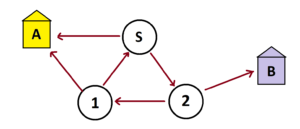
Consider this strange abstract example. (We’ll do some more concrete examples in the next lesson.)

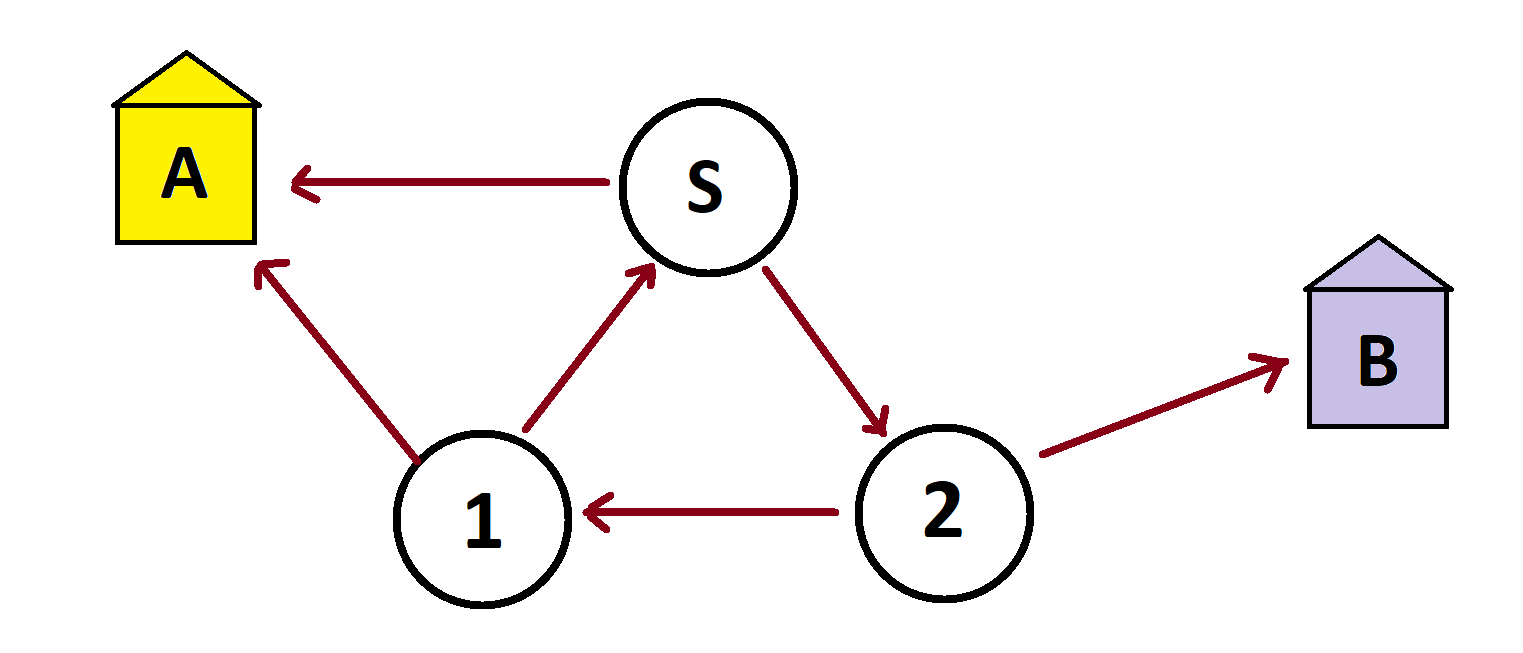
Here an inconceivably large count of people begin in start node S. Half will move straight to house A and half to a node labeled 2.

 

Comment: We see now a standard convention: assume that outgoing edges are equally weighted if they are unlabeled. The two edges out from S thus each have weight \(\frac{1}{2}\).

 

Of those who land in node 2, half will move to house B and half will move to a node labeled 1.

Of those who land in node 1, half will move to house A and half will go back to start to repeat the whole process.

Here are two questions.

 

What proportion of people end up in each house after infinite number if runs of this complex system of paths?

 

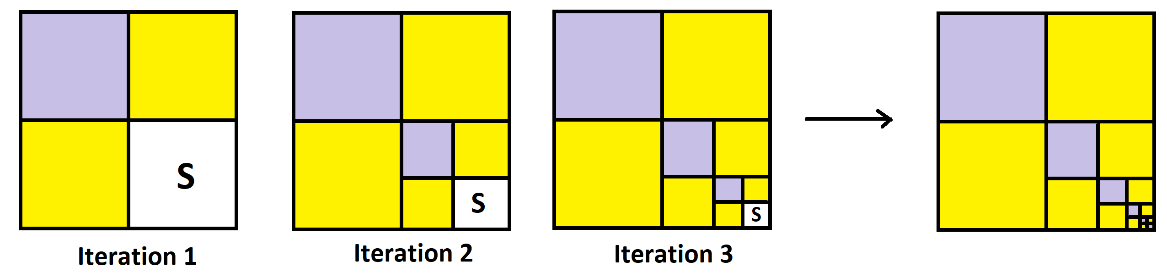
Here’s our area model for a few iterations.

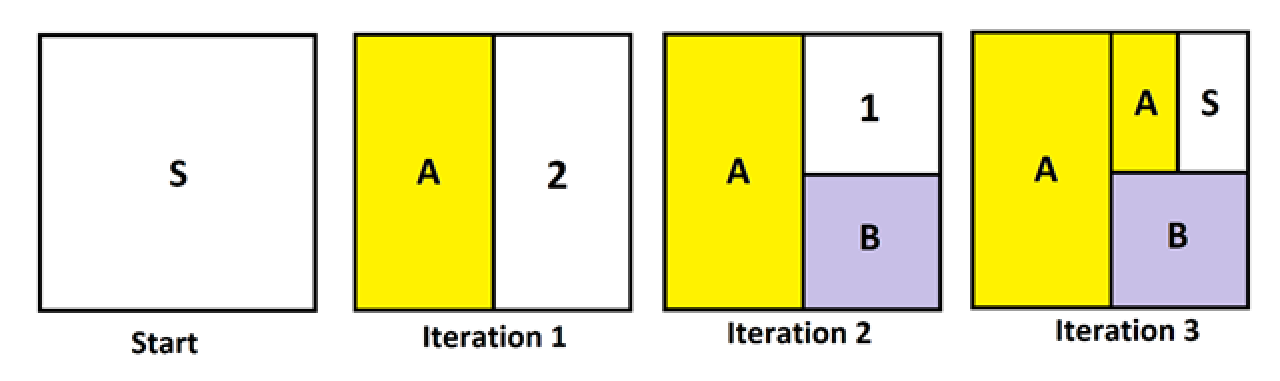
We see that the third iteration brings everyone into a house or back to start. In fact, one-eighth of the people are back at start, five-eighths are in house A, and two-eighths are in house B. It is as though we have been playing with this system.

 

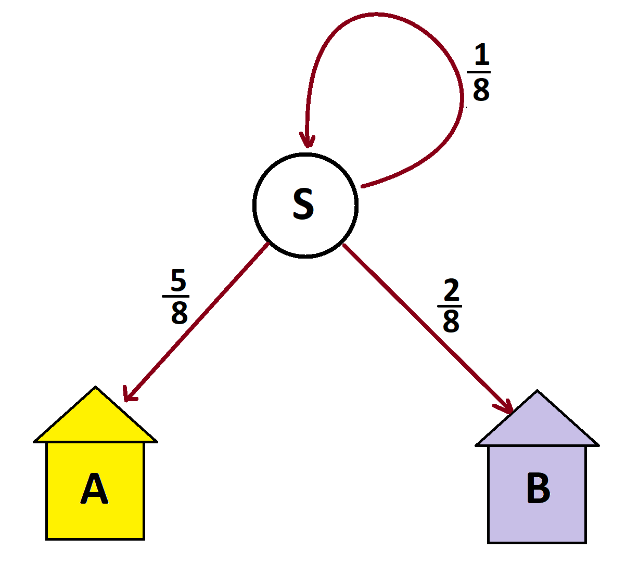
Thus people enter houses A and B in counts of ratio 5 to 2. Since each and every person does eventually enter a house, we see that this philosophically equivalent to this system.

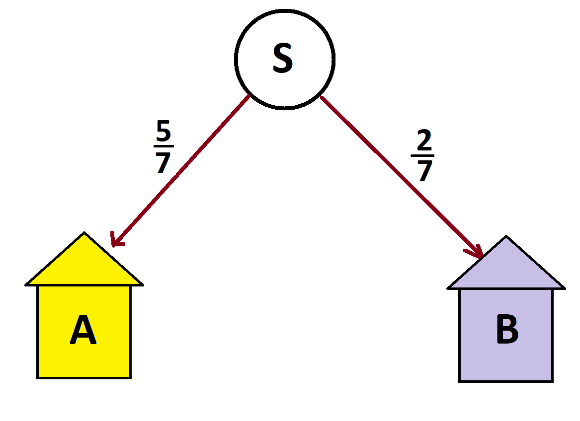
We have that five-sevenths of the people end up in house A and two-sevenths in house B.

 

OPTIONAL: Counting the Expected Number of Steps

Up to now we have been ignoring how many steps it possibly takes people to reach a house. This allowed us to—philosophically—simplify our garden path systems significantly. But let’s now keep track of the number of steps people take. (And now, we are not permitted to simplify the garden paths!)

Here’s a system we’ve seen. We concluded that two-thirds of the people end up in house A and one-third in house B.

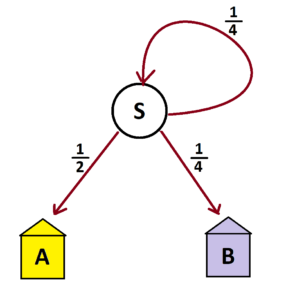
Let’s now go through iterations of this system to see how many steps it takes people to reach a house. After one iteration we have this picture with three-quarters of the people in a house after one step.

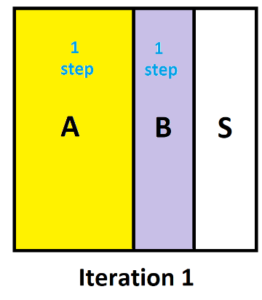
After a second iteration we see that \(\dfrac{3}{16}\) of the people take two steps to land into a house.

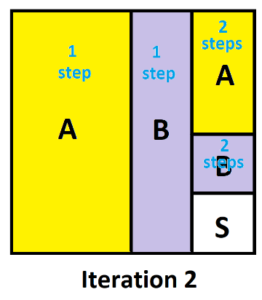
And we see that \(\dfrac{3}{64}\) of the people will take three steps to reach a house after a third iteration. And so on.

 

What is the average number of steps folk take to reach a house?

 

Can we answer this question?  Yes!

Let’ start by giving the unknown average value a name. Most people choose to call it \(m\) for the mean number of steps. From the start state folk will take \(m\) steps to reach a house—on average.

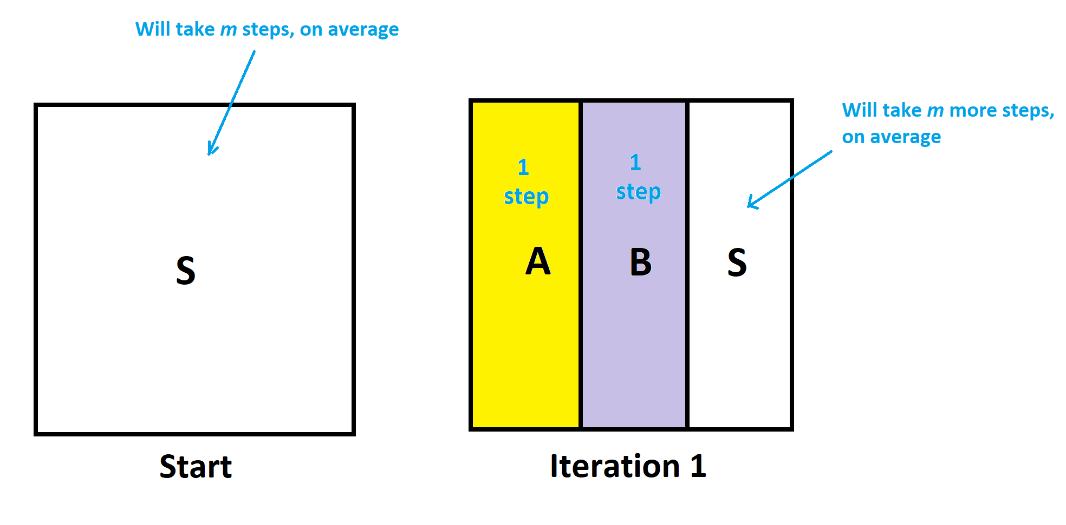
Have everyone take a step.

We see that three-quarters of the people reach a house in just 1 step, and one-quarter of the people will take, on average, an additional \(m\) steps (\(1+m\) steps in total) to reach a house. The average number of steps these people take is

\(\dfrac{3}{4}\left(1\right)+\dfrac{1}{4}\left(1+m\right)\).

 

But these are the same people walking through the same system and so this average must be the same as the original average.

\(m=\dfrac{3}{4}\left(1\right)+\dfrac{1}{4}\left(1+m\right)\).

 

Algebra now gives

\(4m=3+1+m\)

\(3m=4\)

\(m=\dfrac{4}{3}\)

On average, folk take one-and-a-third steps to reach a house!

 

Our First Example: Here it is.

Suppose it take people an average \(m\) on steps to reach a house.

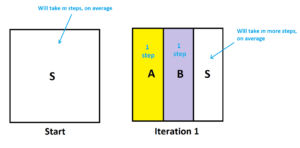
We see that \(m=\dfrac{1}{3}\left(1\right) + \dfrac{1}{3}\left(1\right) +\dfrac{1}{3}\left(1+m\right)\)  giving \(m=\dfrac{3}{2}\).

 

Question: Does it make intuitive sense that, on average, people take more steps to reach a house than the folk in the previous example?

 

 

Our Complicated Example: Here it is.

 

Here are our first few iterations.

 

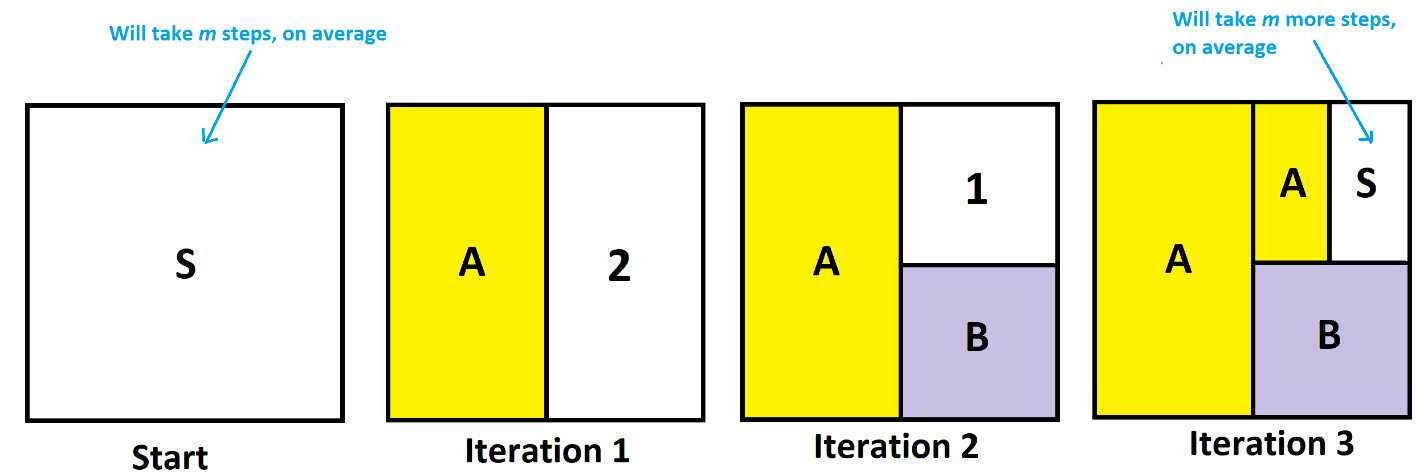
Let \(m\) be the average count of steps people take to end up in a house. The leftmost and rightmost diagram show

\(m=\dfrac{1}{2}\left(1\right)+\dfrac{1}{4}\left(2\right)+\dfrac{1}{8}\left(3\right) \dfrac{1}{8}\left(3+m\right)\).

Solving gives \(m=\dfrac{12}{7}\).

 

Practice Problem 1: Consider the following infinite garden-path system with two types of two-way forks: each fork sends half the people walking through it to a house and the other half to a next fork.

 

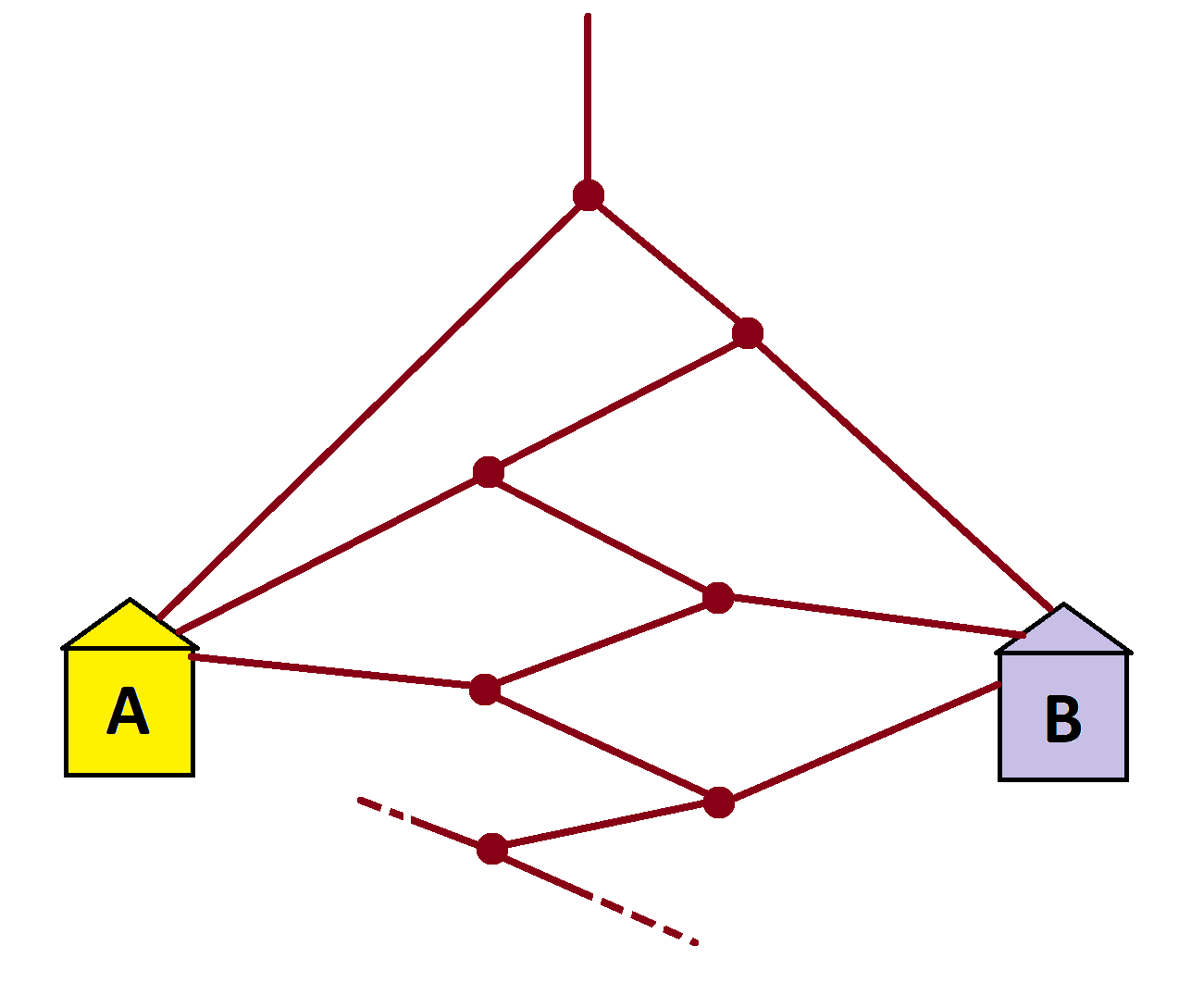
a) Using only a start node S, a second node “1”, and the two houses A and B, redraw this garden path system much more succinctly.

b) In moving though this system, what proportion of people end up in house A and which proportion of people end up in house B?

c) OPTIONAL: On average, how many steps does a person take in moving to a house?

 

 

Practice Problem 2: Here is a very complicated system!

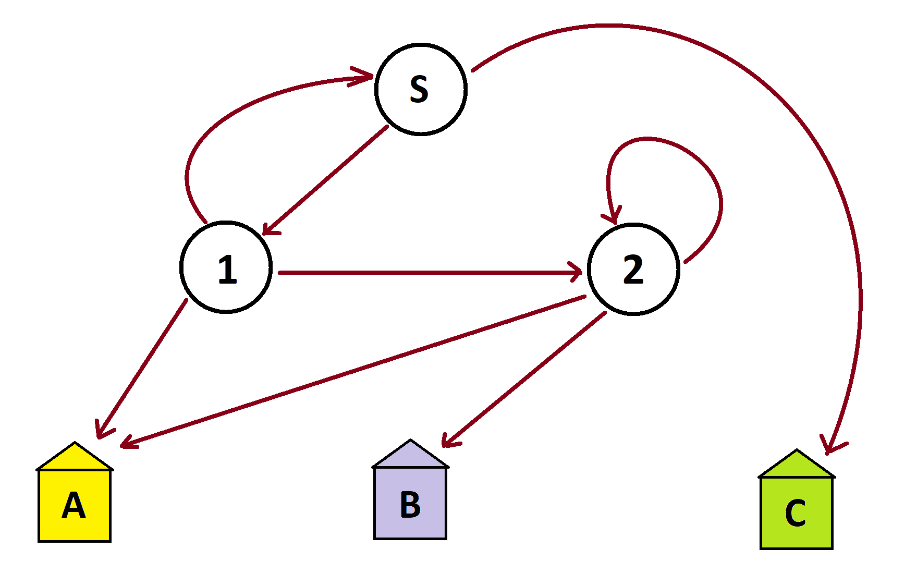
Show that 30% of the people moving through this system will end up in house A, 10% in house B, and 60% in house C.

 

ASIDE ON JARGON

A diagram with nodes, edges, and houses represents what is called an absorbing Markov chain. One imagines an individual roaming about the diagram, starting at one node (which we’ve always labeled S) and choosing to follow an edge from it with probability given by the weights labeled on the edges (or an outgoing edge with equal probability if no weights are given). As soon as person finds herself in a house, she stops, as there are no outgoing edges from a house. (Each house is an absorbing state.)

In this lesson we have been examining the probabilistic motion of a single person roaming about the diagram by imagining the average behavior of an inconceivably large count of people moving through the system. The proportion of people who end up in a particular house matches the probability of an individual within the system landing in that house. And \(m\), the average count of steps people take, is the expected number of steps a person will take before landing in an absorbing state.

 

Resources