Let’s go back to the fun of garden paths for their own sake. And let’s get really wild!

Imagine a garden path with infinitely many forks that each split three ways as shown. Those who turn to the left at a fork go straight to house A, those who turn right to house B, and those who go straight go to another fork. And this is the case over and over and over again!

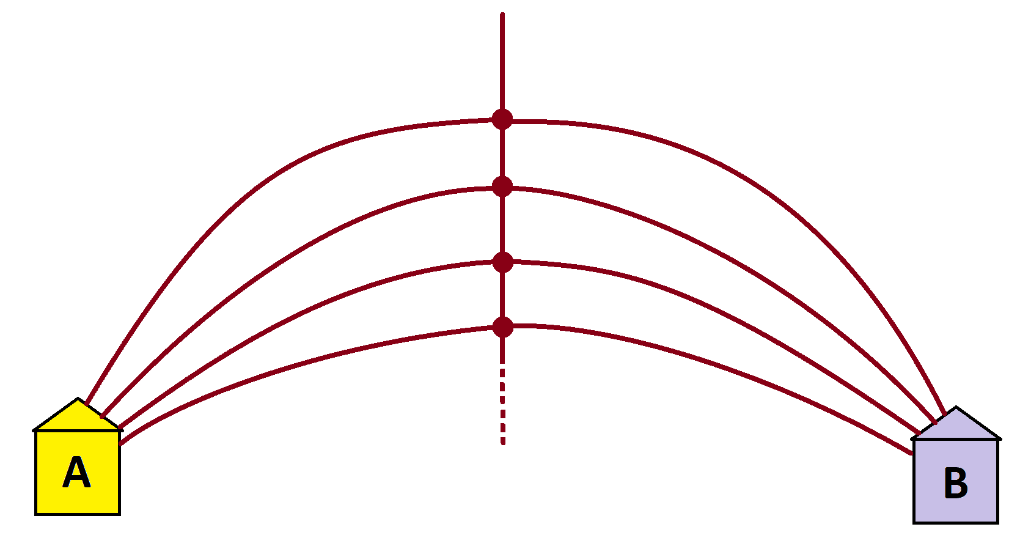
Do you see that this leads to the following picture?

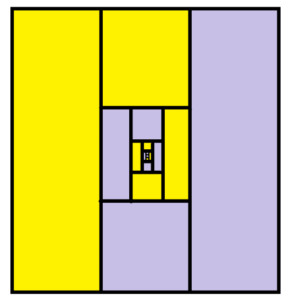
We have two matching spirals that each spiral all the way to the center of the square. Since the spirals are identical, they each take up half the area of the square! So, half the people end up in house A and half the people end up in house B.

But wait! Think of how people end up in house A.

At the first fork,  \(\frac{1}{3}\) of the people go to house A, and a third go to house B, and a third keep going.

Of those who keep going, a third of them (that is, a third of the third, \(\frac{1}{9}\), of the total population) go to house A, a third of the them go to house B, and a third of them keep going.

Of those who still keep going, a third of them (a third of a third of a third, \(\frac{1}{27}\) of the entire population) go to house A, and a third of them go to house B, and a third of them keep going.

And so on.

So we can say that the total number of people who end up in house A must be \(\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{81}+\dfrac{1}{243}+\cdots\).

Yet we said that half the people end up in house A! So this infinitely long sum must equal one half!

\(\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{81}+\dfrac{1}{243}+\cdots=\dfrac{1}{2}\)

Whoa!

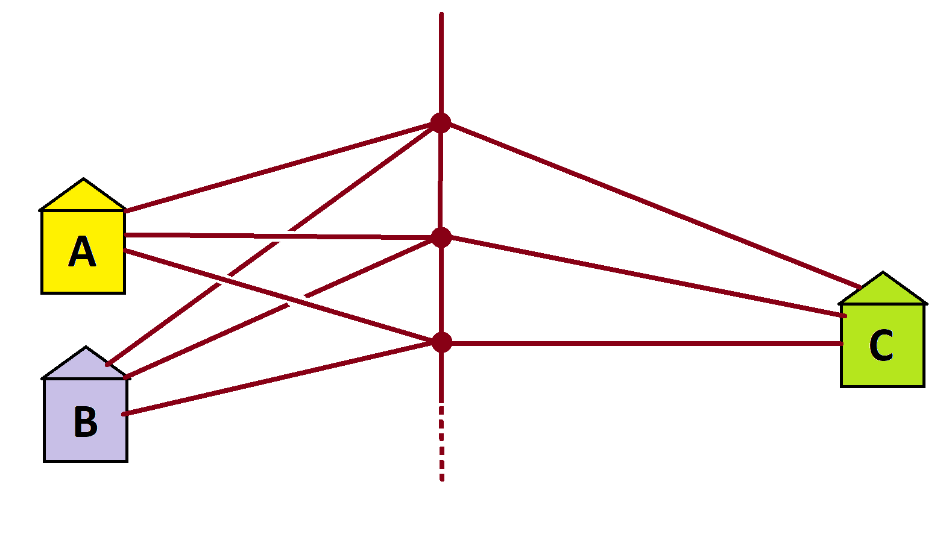
Practice 1:  a) Argue that this next infinite garden path suggests that \(\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{64}+\dfrac{1}{256}+\cdots\)  equals \(\dfrac{1}{3}\).

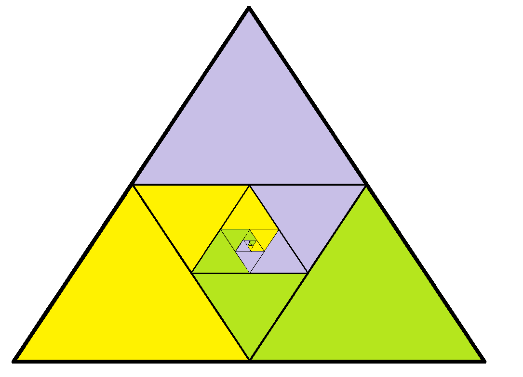
b) Anu was having trouble creating an area model for this system using a square. Then she thought to use an equilateral triangle instead. This is what she drew. What do you think of it?

c) Chee Wei said it is actually possible to use the area of a square to represent this garden-path system nicely. He gave a hint as to what he was thinking by sharing this start to picture on the board. How do you think we will continue the picture?

Practice 2: a) Draw a garden path system that leads to the sum \(\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\dfrac{1}{625}+\cdots=\dfrac{1}{4}\)

b) What do you think might be value of \(\dfrac{1}{N}+\dfrac{1}{N^2}+\dfrac{1}{N^3}+\dfrac{1}{N^4}+\cdots\)for a positive integer \(N\)?

<Answers appear in the Teacher’s Guide>

In Part III we’ll push this example further and open the gates to a whole host of infinite probability processes.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources