Now back to Galileo.

Recall from Lesson 2 that Galileo did confirm experimentally that objects falling (well, rolling) under the influence of gravity accelerate at a constant rate. The data of distances fallen at regular time intervals has constant double differences.

We understand now that Galileo was right to then claim that the data is following a quadratic expression: the height of a falling object is given by a formula of the form

\(at^2+bt+c\)

where  is the amount of time the object has been falling. Wonderful!

 

When one throws an object in the air it undergoes two motions:

i) it moves horizontally at a uniform rate (assuming the effect of air resistance is negligible.

ii) its vertical height changes according to this quadratic formula.

 

The U-shaped curve one sees as the path of a tossed object is, we have now shown, the shape of the graph of a quadratic equation.

 

Parabolas

Greeks scholars of ancient times classified a whole host of special curves following certain geometric properties. One such curve is the parabola, which we alluded to in Lesson 1. It is constructed as follows.

 

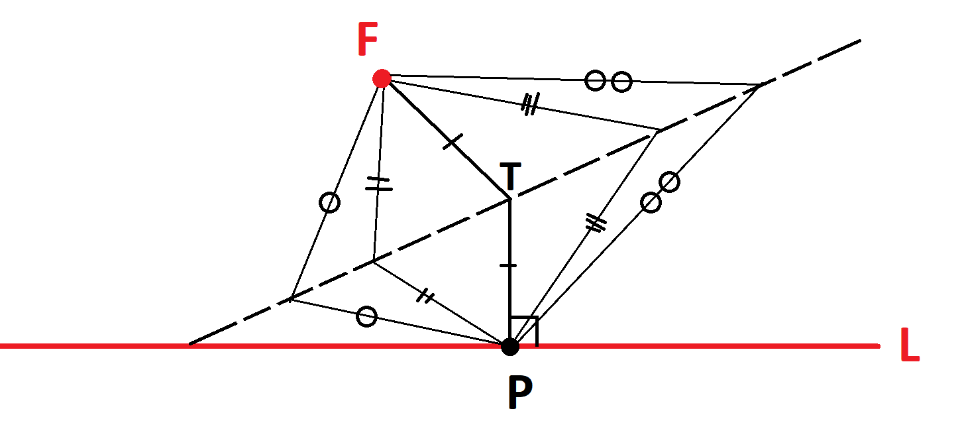
Draw a fixed point \(F\) (called the focus) and a fixed line \(L\)  (called  the directrix) on the page. Then the parabola with this focus and directrix is the set of all points in the plane equally distant from \(F\) and \(L\) as shown.

 

Student Elizabeth Gerber made a parabola on cork board using strings and tacks.

Look at the end of these notes for some additional work of hers. 

 

Legend has it that Archimedes of Syracuse (288 – 212 BCE) suggested building huge parabolic mirrors on the cliffs of the island to focus the Sun’s rays on approaching enemy wooden-ships and set them on fire. Greek scholars knew that the parabolic shape has the geometric property of focusing parallel rays of light.

 

One can construct a parabolic curve by folding paper.

Draw a dot a couple of inches up from the bottom edge of the page for the focus \(F\) and imagine the bottom edge line as the directrix \(L\).

Now lift up the bottom edge and align one point on it with the point \(F\). Make a crease and unfold.

Do this another 50 times or so, lifting different points along the bottom edge up to the point \(F\) and making a crease line each and every time.

Those crease lines outline a curve, and that curve is a parabola!

 

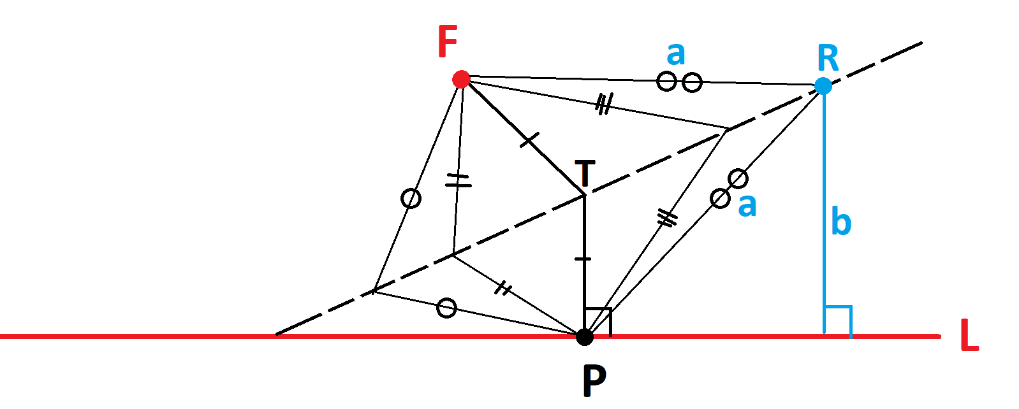
ASIDE: Here’s how to show that the curve we see has the geometric property of being a parabola. To be clear, we will show that each crease line we create is a tangent line to a parabola. The set of all crease lines thus give the set of all tangent lines to the parabola. Suppose the point \(P\) on the directrix is lifted up onto \(F\) to make the dashed crease line shown. By the symmetry of folding, every point on the crease line is the same distance from \(F\) as it is from \(P\). In particular, the point \(T\) directly above \(P\) on the crease line is equidistant from \(P\) and \(F\). We see then that \(T\) satisfies the geometric condition of being on the parabola with focus \(F\) and directrix \(L\). Each crease line has at least one point on the parabola with focus  and directrix . Consider any other point \(R\) on the crease line. Let \(a\) be its distance from \(F\), which equals its distance from \(P\), and let \(b\) be its distance from \(L\). We see that \(b \neq a\) ( \(b\) is the leg of a right triangle and \(a\) is the hypotenuse and these can’t be equal). So \(R\) does not satisfy the geometric condition of being on the parabola with focus \(F\) and directrix \(L\). Each crease line has only one point on the parabola with focus  and directrix .   Thus each crease line meets the parabola with focus \(F\) and directrix \(L\) at only one point, and so is indeed a tangent line to the curve.

 

ACTIVITY:

High school textbooks make the claim that a parabola is the same shape curve as the graph of a quadratic equation \(y=ax^2+bx+c\). Does this seem feasible?

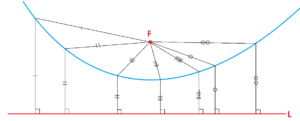
1. Make a parabola by folding paper.

2. Mark off regular intervals along the bottom edge and measures heights from the bottom edge to the curve as shown. This gives a sequence of values.

3. Compute the difference table for this data.

4. Within human error, does it seem reasonable to say that you have constant double differences?

 

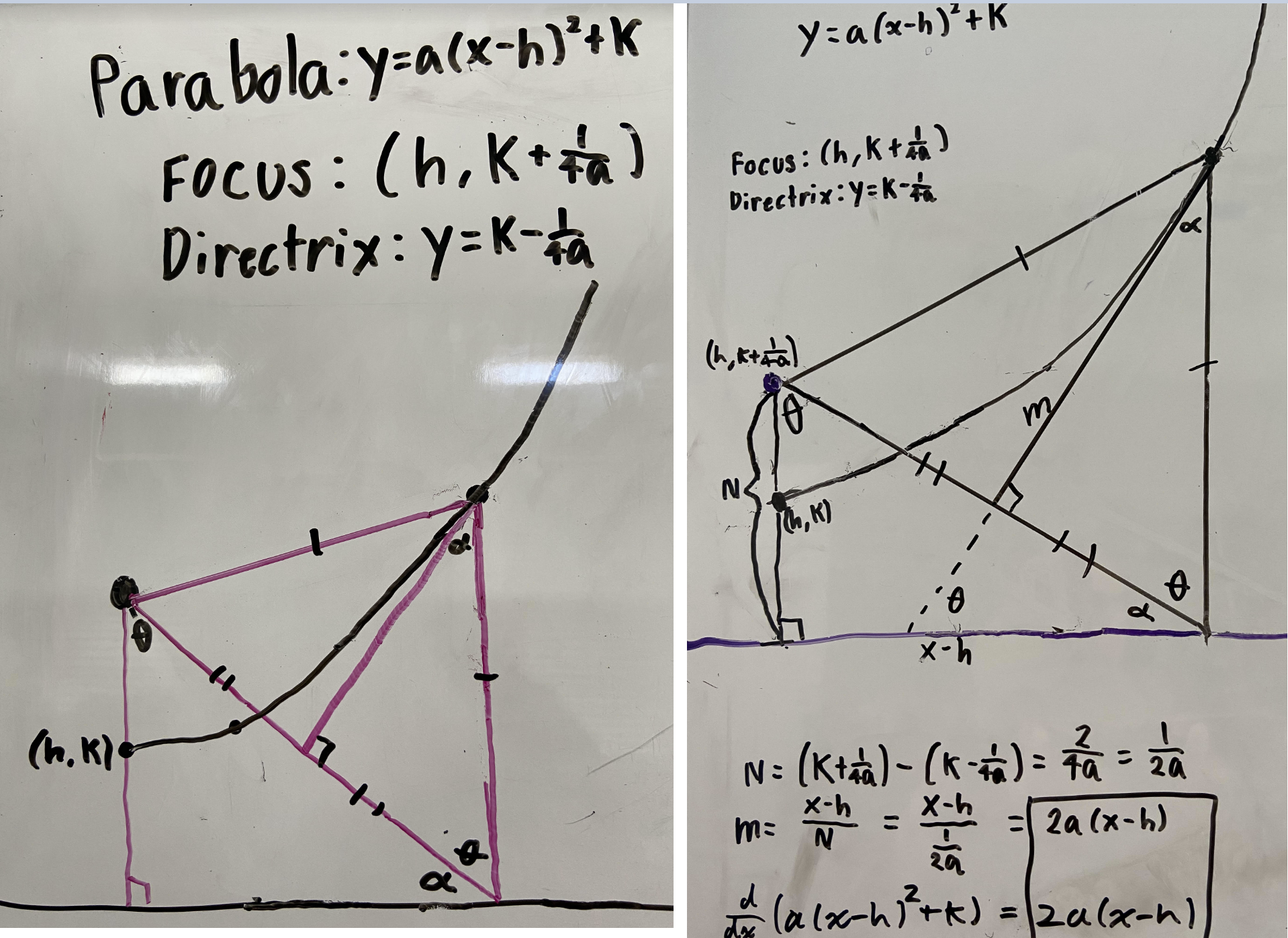
CHALLENGE: Suppose we situate matters in the coordinate plane so that the directrix \(L\) is a horizontal line \(k\) units below the \(x\)-axis (and so has equation \(y=-k\)) and the focus \(F\) is a point \(k\) units high on the vertical axis (and so has coordinates \((0,k)\)).

Translate the geometric condition for a point \(P=(x,y)\) to be the parabola with focus \(F\) and directrix \(L\) into an algebraic condition. Is that algebraic condition a quadratic equation?

HARD CHALLENGE:  Conversely, prove the graph of a quadratic equation \(y=ax^2+bx+c\) is sure to be a parabola. What is its focus? What is it is directrix?

 

Pedagogical Comment: This is a common faux pas of many high school texts. It is taken as “obvious” that the terms parabola and quadratic graph are interchangeable. The definition of a parabola is very different from the definition of the graph of an equation  \(y=ax^2+bx+c\) and it is not at all obvious that these two curves are, or even should be, the same.

Galileo’s Mis-step

Let’s keep studying the U-shaped curves we see in nature.

Galileo noticed that the shape of chain hanging between two poles follows a U-shaped curve and wondered if it is following a basic quadratic formula too. He suspected it did.

 

ACTIVITY:

1. Hang a piece of light-weight chain on a white-board.

2. With a ruler, draw a horizontal line and mark off regular intervals along it. Measure the horizontal heights shown and collect a sequence of data values.

3. Use difference methods to find a quadratic formula for the heights along the chain. Be honest about what you notice.

 

 

 

DO NOT READ THE NEXT SECTION UNTIL YOU HAVE ACTUALLY TRIED THIS ACTIVITY FOR YOURSELF AND HAVE LOOKED AT YOUR OWN DATA. (Spoilers are coming next!)

 

There are no doubt inaccuracies in your data due to human error and the first and second differences you calculate are not constant. Go back and try to collect more precise and accurate data.

 

But you will find the second differences are still not constant.

And try as you might, with more and more accurate measurements, you will fail to see constant second differences.

 

It turns out that the U-shaped curves of hanging chains simply are not quadratic. And your data is telling you that!

The shape of the curve of a hanging chain is known as a catenary curve (from the Latin catena for chain). It wasn’t until 1691 that mathematicians found a precise formula for this curve—and it is very different from a quadratic expression!

 

To end this lesson, let me point out that you how have the practical power to test whether or not certain U-shape curves are actually quadratic in structure. Feel free to try these four examples.

 

EXTENDED ACTIVITY 1: Is the St. Louis Gateway Arch in the shape of a quadratic curve? Find out by making measurements on a photograph of the arch.

EXTENDED ACTIVITY 2: Is a semi-circle given by a quadratic expression? Find out by tracing a pot lid on a piece of paper and making measurements with a ruler.

EXTENDED ACTIVITY 3: Is the shape of a rainbow given by a quadratic expression. Find a photograph of a rainbow and collect data from it.

EXTENDED ACTIVITY 4: Is the path of a projectile truly quadratic (or does air resistance have a significant effect on the shape of paths)? Find a time-lapse series of photographs of a basketball or some other tossed object and measure the height of the ball on the photographs at regular time intervals.

 

 

Comment: Here’s a shocker. The path of a projectile on the surface of a planet—even one without an atmosphere, which avoids air resistance—is never quadratic in nature! The motion of a thrown object in ideal circumstances is actually the arc of ellipse, another different curve identified by Greek scholars of ancient times.

The underlying assumption in physics classes is that the Earth is flat and that gravity always points pulls in the same direction. But on a spherical planet the direction of the “pull” of gravity is always towards the center of the planet, and this direction changes as the object moves.

 

Shout Out to Elizabeth G. and her brother Victor G.

Using the tools of geometry–angle bisectors, equidistance, slopes of perpendicular lines–Elizabeth and her brother were able to find a formula for the slope of the tangent line to a parabola, the same  formula that calculus gives. They were also able to prove that, indeed, parallel rays of light reflect off a parabolic surface to meet at its focus.

 

Resources