When I teach trigonometry, be it for first-timers starting high-school, or high-schoolers in an upper-level course, or adults getting going on their math education, I always start by telling the human history story of the subject as I detail below (though I am a bit loose with the story — see the warning below). In my humble opinion, the standard curriculum presents it kinda backwards: circle-ometry is the natural starting point for this wonderful subject, with trigonometry coming as the after-focus, just as the human history story tells it. The history of math, by-and-large, reveals how our individual brains naturally come to understand math – again, in my humble opinon.

So perhaps try sharing and discussion each of these videos in turn with your students, with no pressure to attend to mastery in any way: just take in the story and dabble with the math itself as much as feels good and fun. Places to naturally tie it all with your current curriculum will come up – even if it is at the and when we finally get to SOHCAHTOA and all that. 

Just have fun discussing with your fabulous students!

UPDATE: Other fabulous educators are starting to chime in with materials and videos to share on their takes and their advice on actually implementing this story of trigonometry in their classrooms. Let’s use this page as a start to collating materials and I’ll organise a proper independent unit created by our community when we’re in good shape. For now, scroll to the end and avoid all this Tanton stuff! 

 

Video 1: INTRODUCTION 

Most every one has heard of this thing called “trigonometry” and are vaguely aware that it has something to do with triangles and ratios and curious names for these ratios. Let’s start by putting all that aside!

Is This Sounding Too Radical for your Department Expectations? 

Then skip all this human story and connection and try this more traditional approach to the subject, leaning straight into right triangles and the expected immediate content.

SOH and CAH and then TOA_An alternative introduction

 

Video 2: Circle-ometry

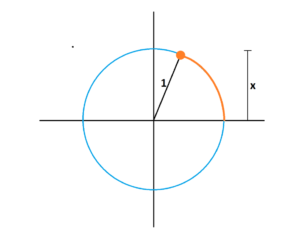
Let’s’ go back to the dawn of time and ask some fundamentally human questions. Everything is about understanding the motion of the Sun and other heavenly bodies. Plus .. we’ll hear about a quirky mishap in translation that leads us to talk about the “twisty bit” of the Sun (it’s sine!), even though that literally makes no sense!

WARNING: I am a bit too loose and wild in my story here. I am pretty much right on with what is known, for sure, about the historical development of the subject–a focus on circles and chords and half chords, how sine got its name, for example–and but some extra bits and pieces I offer are based on popular conjectures about what people were thinking and not pinned down by mathematical historians as certain–why exactly we prefer clockwise motion in math, why exactly we chose to draw axes as we do.   

Your Project: Check on me! What exactly do historians know for sure and say about all the ideas presented?  

Video 3: Some Basic Trigonometric Observations

Usually reserved for upper-level trigonometry, some basic trig identities are just natural when seen in the human story of circle-ometry.

Video 4: The Story Continues

Now we’re going to see what happened to change “circle-ometry” into trigonometry. It’s late in this story of human history, but it brings us to the start of how most people are introduced to the topic.

Video 5: Explaining the Names TANGENT and SECANT

Have you ever noticed that these are geometry words? What has “opp/adj” got to do with a tangent line? What has “hyp/adj” got to do with a secant line? There is natural sense to all this!

Have a look at this NumberPhile video by the the inimitable Ben Sparks. See all these circular functions in action!

Video 6: ASIDE: \(\dfrac{1}{\sqrt{2}}\) versus \(\dfrac{\sqrt{2}}{2}\)

I promised to address this issue in the second video. Why did it once help to put square roots on top? Does it still help today?

 

 

Video 7: DEGREES and RADIANS

Who chose the number 360 for the count of degrees in a circle? Is that number natural to math or unnatural? Would Martians choose this count too? Does mathematics “want” this count?

 

 

Video 8: Graphing Trig Functions

A sine wave is simply circular motion viewed sideways. As circular motion is natural to the universe, sine waves are too.

 

Video 9: SQUINE and COSQUINE

Actually, who said motion had to be circular? Let’s have some quirky fun!

Video 10: Fitting Trig Functions to Data

Things that seem to wax and wane in a cyclic fashion might well be modelling with a trigonometric function.

Video 11: The SUM and DIFFERENCE FORMULAS (and why complex numbers reveal that trig identities are really just easy exponent rules in disguise!)

We have to do it – the sum and difference formulas, the double-angle formulas, and such. (And then I reveal what I personally have in my head re all this.)

Video 12: The Law of Cosines; The Area of a Triangle; The Law of Sines

The content keeps going! Here are some fun ways to ponder on some classic trigonometric theorems.

Short Chapter 12: Inverse Trig Functions

I didn’t make a video for this one, but here is my take on using circle-ometry to make natural sense of the inverse trigonometric operations \(arcsin\), \(arccos\), and such (aka \(sin^{-1}\), \(cos^{-1}\), etc.) Here there are no “ambiguous” cases to consider.

Trigonometry Short Chapter_Inverse Trig Functions

 

GLOBAL COMMUNITY CONTRIBUTIONS

From Rosalind Carson

Rosalind Carson has been using this historical approach to teaching trigonometry with students and has created content to start giving some nuts-and-bolts to what one actually does in the class.

STUDENT WORKSHEET 1: Rosalind has created a worksheet to match my first video on “circle-ometry”:

RCs handout trigonometry 1.1

TEACHER VIDEO 1: Her first video for teachers (below) bounces off of–and improves!–my approach above.

DID YOU WATCH IT QUIZLETTE? ASU Mathematical Academic Professional Casey Warmbrand had the idea of creating a quick Google Survey to make sure his students watched Rosalind’s video. 

 

TEACHER VIDEO 2: Her second video starts looking at some trigonometric identities.

STUDENT WORKSHEET 2: Rosalind has created a worksheet to follow this second video.  Handout Trig 1.2

TEACHER VIDEO 3: The Law of Cosines and the Law of Sines

TEACHER VIDEO 4: Sum and Difference formulas (aka Ptolemy’s Formulas)

 

About Rosalind:

Rosalind Carson is a Mathematics Education Consultant with an M.Sc. in Curriculum and Instruction and Permanent Teaching Certificate in Alberta, Canada. She started her career as a high school mathematics teacher in Calgary.  She was a Learning Specialist in Mathematics for the Rocky View School Division. For the past 10 years, Rosalind has worked with kindergarten to high school mathematics teachers, presented school, divisional, and regional professional development seminars, webinars and workshops.  She continues to learn the historical roots of mathematical content and  strives to bring historical and holistic approaches to mathematics teaching. 

From Kiran Bacche

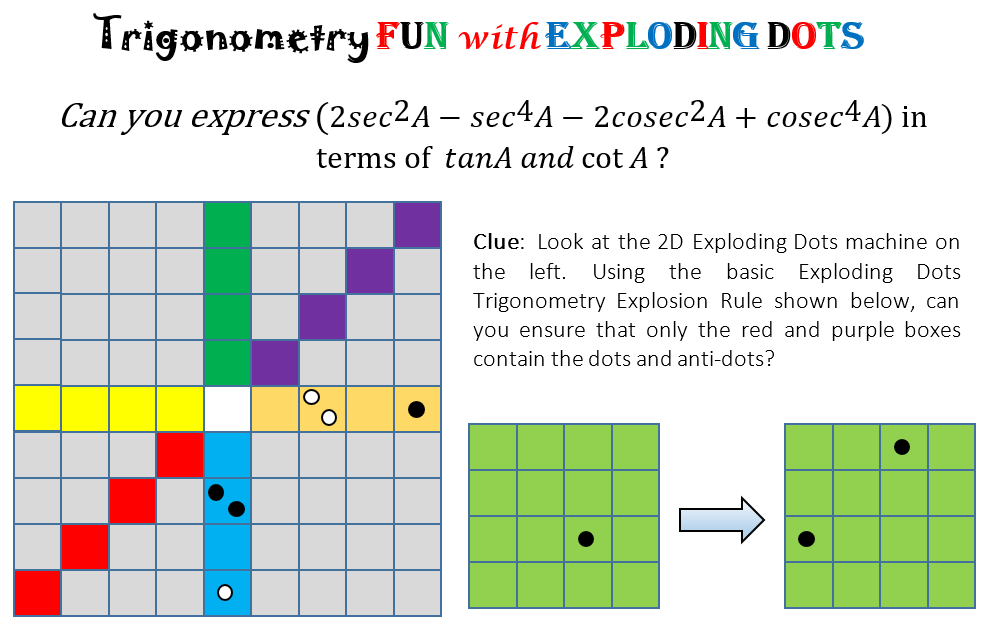
Kiran is an author, a math outreach practitioner, a software engineer, and  ambassador for the Global Math Project from Bangalore, India, and has formulated the incredible insight that the majority of “prove this trig identity” problems we give to students can be well handled with a two-dimensional version of Napier’s Checkerboard from Exploding Dots.

Here’s a document explaining the lovely approach!

Kiran B_Trig Identity Worksheet

 

A puzzle fully explained in the worksheet.

 

 

 

 

 

 

Resources